Todennäköisyys
Oppimisen Tavoite(s)
· Määrittää tapahtuman, tulos, oikeudenkäynti, yksinkertainen tapahtuma, näyte tila ja laskea todennäköisyys, että tapahtuma esiintyy.
· Laske todennäköisyys tapahtumia monimutkaisempia tuloksia.
· ratkaise sovelluksia, joissa on todennäköisyyksiä.
Johdanto
Todennäköisyys tarjoaa mitata, kuinka todennäköistä on, että jotain tapahtuu., Se on numero välillä ja myös numerot 0 ja 1. Se voidaan kirjoittaa murto-osaan, desimaaliin tai prosenttiin.

Poiminta numeroita satunnaisesti tarkoittaa, että ei ole olemassa mitään erityistä järjestyksessä, jossa ne on valittu. Monet pelit käyttävät noppia tai spinnereitä numeroiden tuottamiseen satunnaisesti. Jos et ymmärtää, miten laskea todennäköisyyksiä, voit tehdä harkittuja päätöksiä siitä, miten pelata näitä pelejä tietäen todennäköisyys eri tuloksia.,
Määritelmiä
Ensimmäinen, sinun täytyy tietää joitakin termejä, jotka liittyvät todennäköisyys. Todennäköisyydellä työskenneltäessä satunnaista toimintaa tai tekojen sarjaa kutsutaan kokeiluksi. Lopputulos on oikeudenkäynnin tulos, ja tapahtuma on erityinen tulosten kokoelma. Tapahtumat on yleensä kuvattu käyttämällä yhteistä ominaisuutta tuloksia.
sovelletaan tätä kieltä nähdä, miten termit toimivat käytännössä. Jotkut pelit vaativat liikkuvan kuolee kuusi puolta, numeroitu 1-6. (Dice on monikko die.,) Alla oleva kaavio kuvaa käyttää oikeudenkäynnin lopputulokseen, ja tapahtuma tällainen peli:
Huomaa, että kokoelma tuloksia on laittaa olkaimet ja pilkuilla.
yksinkertainen tapahtuma on tapahtuma, jossa on vain yksi lopputulos. Rolling 1 olisi yksinkertainen tapahtuma, koska on vain yksi tulos, joka toimii-1! Liikkuvan enemmän kuin 5 voisi myös olla yksinkertainen tapahtuma, koska tapahtuma sisältää vain 6 kelvollinen tulos. Yhdistetapahtuma on tapahtuma, jossa on useampi kuin yksi lopputulos. Esimerkiksi liikkuvan yksi kuusi puolinen die, liikkuvan jopa numero voi esiintyä yksi kolmesta tuloksia: 2, 4 ja 6.,
Kun heität kuusisivuinen kuolla monta kertaa, sinun ei pitäisi odottaa tahansa lopputulos tapahtua useammin kuin toinen (olettaen, että se on oikeudenmukainen die). Tulosten tällaisessa tilanteessa sanotaan olevan yhtä todennäköisiä. On erittäin tärkeää tunnistaa, milloin tulokset ovat yhtä todennäköisiä laskettaessa todennäköisyyttä. Koska jokainen tulos die liikkuvan oikeudenkäynti on yhtä todennäköisesti, voit odottaa saada jokainen tulos ![]() rolls., Että on, voit odottaa
rolls., Että on, voit odottaa ![]() rolls olla 1,
rolls olla 1, ![]() rolls olla 2,
rolls olla 2, ![]() rolls olla 3, ja niin edelleen.
rolls olla 3, ja niin edelleen.
kehrääjä on jaettu neljään yhtä suureen osaan, joista jokainen on värillinen erivärisellä kuten alla on esitetty. Kun tämä kehrääjä kehrätään, nuoli osoittaa yhteen väreistä. Ovatko tulokset yhtä todennäköisiä?
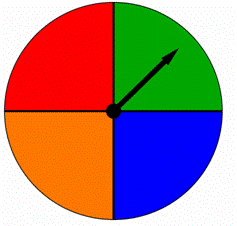
A) Kyllä, he ovat yhtä todennäköisiä.
B) ei, ne eivät ole yhtä todennäköisiä.,
Todennäköisyys Tapahtumia,
todennäköisyys, Että tapahtuma on, miten usein se on odotettavissa. Se on tapahtumatilan koon suhde näytetilan kokoon.
ensin pitää määrittää näyteavaruuden koko. Näyteavaruuden koko on mahdollisten tulosten kokonaismäärä. Esimerkiksi, kun rulla 1 kuolee, näyte tila on 1, 2, 3, 4, 5, tai 6. Näytetilan koko on siis 6.
sitten sinun täytyy määrittää tapahtumatilan koko., Tapahtumatila on se, kuinka monta lopputulosta on tapahtumassa, josta on kiinnostunut. Tapahtumatila alle kolmosen pyörittämiselle on 1 tai 2. Tapahtumatilan koko on siis 2.
yhtä todennäköisten tulosten osalta tapahtuman e todennäköisyys voidaan kirjoittaa P(E).
![]()
|
Esimerkki |
||
|
Ongelma |
peli vaatii liikkuvan kuusi puolinen die numeroitu 1-6., Mikä on todennäköisyys rullata parillinen määrä? |
|
|
Näyte tilaa = {1, 2, 3, 4, 5, 6}
Tapahtuman tilaa = {2, 4, 6} |
Ensimmäinen, löytää otosavaruuden ja tapahtuman tila. Näytetila on kaikki mahdolliset lopputulokset, ja tapahtumatila on tapahtuman lopputulokset. Tällöin tapahtuma ” pyörittää parillista lukua.,” |
|
|
|
Koska tulokset ovat yhtä todennäköisiä, todennäköisyys, että tapahtuma on suhde tapahtuman tilaa näyte tilaa., |
|
|
Vastaus |
P(parillinen määrä) = |
|
– Se on yleinen käytäntö, jossa todennäköisyydet, kuten jakeet yleensä yksinkertaistaa todennäköisyydellä osaksi alhaisin vuodesta, joka tekee se helpompaa varten useimmat ihmiset saada käsityksen siitä, kuinka suuri se on. Ellei ole syytä olla tekemättä niin, ilmaise kaikki lopulliset todennäköisyydet pienin termein.,
kiekko on jaettu samoihin osiin, joista jokainen on värillinen erivärisellä kuten alla on esitetty., Löytää todennäköisyys spinning sininen tai vihreä tätä kiekkoa:
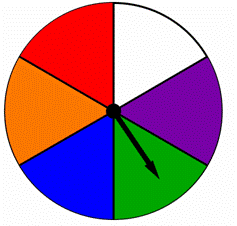
A) ![]()
B) ![]()
C) 2
D) 6
Laskenta Menetelmiä löytää Näyte Tiloja,
vaikeinta laskettaessa todennäköisyys voidaan löytää koko otosavaruuden, varsinkin jos on kaksi tai enemmän kokeita. On olemassa useita laskentamenetelmiä, jotka voivat auttaa.,
ensimmäinen, jota tarkastellaan, tekee kaavion. Alla olevassa esimerkissä Tori pyörittelee kahta kolikkoa. Joten sinun täytyy määrittää näytteen tila huolellisesti. Seuraavassa esimerkissä esitetyn kaltainen kaavio on hyvä lähestymistapa.
|
Esimerkki |
||||
|
Ongelma |
Tori on flipping pari kolikkoa ja huomata, kuinka paljon voltteja ja ”päät”, hän saa. Mikä on todennäköisyys, että hän kääntää 2 päätä?, Mikä on todennäköisyys, että hän kääntää vain 1 pää?,15ecf6″>T |
T |
TT |
|
sample space: {HH, HT, TH, TT}
event space for 2 heads: {HH}
event space for 1 head: {HT, TH}
Create a chart to record the results of flipping the first coin, followed by the result of flipping the second coin.,
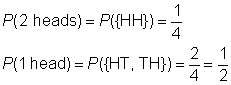
Koska tulokset ovat yhtä todennäköisiä, todennäköisyys, että tapahtuma on suhde tapahtuman tilaa näyte tilaa.,
Vastaus
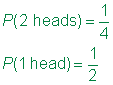
alla olevassa esimerkissä näyte tilaa Tori on yksinkertainen kuin vain yhtä noppaa on rullattu. Koska James kuitenkin pyörittelee kahta kuolonuhria, kaavio auttaa tiedon järjestämisessä.,
|
Esimerkki |
||||||||
|
Ongelma |
Tori rullattu kuusisivuinen kuolla ja halusi saada seurausta joko 1 tai 4. James pyöräytti kaksi kuusisivuista noppaa, yhden sinisen ja yhden punaisen, ja halusi saada tuloksen sekä 1 että 3, samaan aikaan. Millä tapahtumalla on suurempi todennäköisyys?, |
|||||||
|
Tori’s sample space: {1, 2, 3, 4, 5, 6}
Tori’s event space: {1, 4}
Tori:
|
First, find the sample space and the event space for the two trials., Torin oikeudenkäynnin kannalta tämä on suoraviivaista. Koska tulokset ovat yhtä todennäköisiä, todennäköisyys, että tapahtuma on suhde tapahtuman tilaa näyte tilaa.,316594724″> 6 |
6,1 |
6,2 |
6,3 |
6,4 |
6,5 |
6,6 |
|
James’ sample space has 36 outcomes.,
Jamesin tapahtuma-alueella on 2 lopputulosta.
se ei ole Jamesin oikeudenkäynnissä niin ilmeinen, sillä hän heittää kaksi noppaa. Käytä kaaviota löytää mahdollisuuksia.
tuloksia on 36. Näistä on 2, joilla on sekä 1 että 3.,
James: ![]()
Koska tulokset ovat yhtä todennäköisiä, todennäköisyys, että tapahtuma on suhde tapahtuman tilaa näyte tilaa.
Vastaus
Tori-tapahtuma on suurempi todennäköisyys.,
Voit myös käyttää puu kaavio määrittää näytteen tilaa. Puukaaviossa on oksa jokaiselle mahdolliselle tapahtumalle.
Oletetaan, että kaapissa on kolmet housut (musta, valkoinen, ja vihreä), neljä paitaa (vihreä, valkoinen, violetti ja keltainen), ja kaksi paria kenkiä (musta ja valkoinen). Kuinka monta erilaista asua voi tehdä? Housuihin on 3 vaihtoehtoa, paitoihin 4 vaihtoehtoa ja kenkiin 2 vaihtoehtoa., Meidän puu kaavio, katsotaanpa käyttää B musta W valkoinen G, vihreä, P violetti, ja Y keltainen.
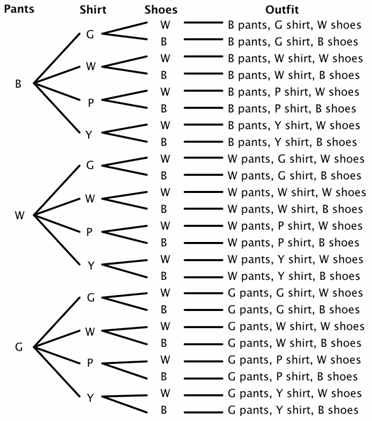
Voit nähdä puu kaavio, joka on 24 mahdollista asuja (jotkut ehkä ole suuria valintoja) näytteen tila.
Nyt voit melko helposti ratkaista joitakin todennäköisyys ongelmia. Mikä on esimerkiksi todennäköisyys, että jos sulkee silmänsä ja valitsee sattumanvaraisesti, valitsisi samanväriset housut ja kengät? Voit nähdä, että on 8 asuja, joissa housut ja kengät sopivat.,
![]()
Kun olet nähnyt, kun oikeudenkäyntiin osallistuu useampi kuin yksi satunnainen elementti, kuten flipping enemmän kuin yhden kolikon tai liikkuvan enemmän kuin yksi kuolee, et aina täytyy tunnistaa jokainen tulos näyte tilaa laskea todennäköisyys. Tarvitset vain määrän tuloksia.
keskeinen Laskennan Periaate on tapa löytää määrä tuloksia ilman listalle ja laskee jokaisen.,
keskeinen Laskennan Periaate
Jos yksi tapahtuma on p mahdollisia tuloksia, ja toinen tapahtuma on m mahdollista lopputulosta, niin on olemassa a yhteensä p • m mahdollisia tuloksia kahden tapahtumia.
Esimerkkejä
· Liikkuvan kaksi kuuden sivuinen noppa: Jokainen kuolee on 6 yhtä todennäköisiä, joten näytteen tila on 6 • 6 tai 36 yhtä todennäköisiä.
· Käännetään kolme kolikkoa: Jokainen kolikko on 2 yhtä todennäköisiä, joten näyte tilaa on 2 • 2 • 2 tai 8 yhtä todennäköisiä.,
· Liikkuvan kuusi puolinen die ja kolikonheittoa: näytteen tila on 6 • 2 tai 12 yhtä todennäköisiä.
joten voit käyttää perustavaa Laskentaperiaatetta selvittääksesi, kuinka monta asukokonaisuutta edellisessä esimerkissä on. Housuihin on 3 vaihtoehtoa, paitoihin 4 vaihtoehtoa ja kenkiin 2 vaihtoehtoa. Käyttämällä peruslaskenta periaate, olet 4 • 3 • 2 = 24 erilaista asua.,
|
Esimerkki |
||
|
Ongelma |
Barry vapaaehtoisten hyväntekeväisyys kävellä, jotta lounaat kaikille muille vapaaehtoisille. Jokaisen pussin hän laittaa: · kaksi voileipiä (maapähkinävoita ja hyytelöä, tai kalkkuna ja juusto), · yksi kolmesta pelimerkkejä (säännöllinen peruna sirut, paistettu peruna pelimerkkejä, tai maissi pelimerkkejä), · yksi pala hedelmää (omena tai appelsiini)., hän unohti merkitä, mitä laukuissa oli. Olettaen, että jokainen valinta on yhtä todennäköistä, mikä on todennäköisyys, että pussissa Therese saa omistaa maapähkinävoi ja hyytelöä voileipä ja omena?, |
|
|
Size of sample space:
(number of sandwich choices) • (number of chip choices) • (number of fruit choices) = 2 • 3 • 2 = 12
|
First, use the Fundamental Counting Principle to find the size of the sample space., |
|
|
Koko tapahtuman tila:
(numero sandwich valintoja tapahtuma) • (määrä siru valintoja tapahtuma) • (määrä hedelmiä valintoja tapahtuma) = |
tapahtuman tilaa, noudattaa samaa periaatetta. Tällöin tarjolla on vain yksi voileipä ja yksi kiinnostava hedelmä, mutta mikä tahansa kolmesta sirutyypistä on hyväksyttävää., |
|
|
Vastaus |
|
Käytä suhde löytää todennäköisyys. |
Carrie kääntyy neljä kolikot ja laskee useita hännät. On neljä tapaa saada täsmälleen yksi pyrstö: HHHT, HHTH, HTHH, ja THHH. Mikä on todennäköisyys, että Carrie saa täsmälleen yhden hännän?,
A) ![]()
B) ![]()
C) ![]()
D) ![]()
Summary
Probability helps you understand random, unpredictable situations where multiple outcomes are possible., Se on tapahtuman todennäköisyyden mittari, ja se riippuu tapahtuman ja mahdollisten tulosten suhteesta, jos kaikki nämä tulokset ovat yhtä todennäköisiä.