Julkisen Avaimen Salaus

Julkisen Avaimen Salausta

toisin Kuin symmetrisen avaimen salaus, emme löydä historiallisia käyttää julkisen avaimen salausta. Se on suhteellisen uusi käsite.

Symmetrinen salaus on soveltuu hyvin organisaatioille, kuten hallitusten, armeijan, ja iso rahoituslaitokset olivat mukana luokiteltu viestintä.,

Kanssa leviämisen enemmän suojaamattomia tietoverkkojen viime vuosikymmeninä, todellinen tarve tuntui käyttää salausta klo suuremmassa mittakaavassa. Symmetrisen avaimen todettiin olevan epäkäytännöllinen, koska sillä oli haasteita avainhallinnassa. Tämä synnytti julkisen avain cryptosystems.

prosessi salaus ja salauksen purku on kuvattu seuraavassa kuvassa.

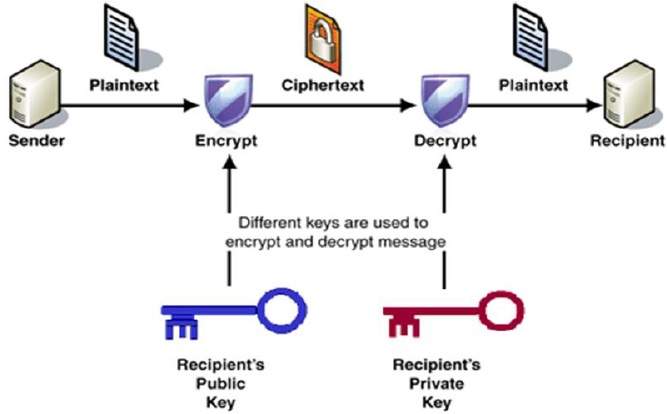
tärkeimmät ominaisuudet julkisen avaimen salaus järjestelmä ovat −

• Eri avaimet, joita käytetään salaukseen ja salauksen., Tämä on ominaisuus, joka asettaa tämän järjestelmän erilainen kuin symmetrinen salausjärjestelmä.

• jokaisella vastaanottajalla on käytössään ainutlaatuinen salausavain, jota yleensä kutsutaan hänen yksityisavaimekseen.

• Vastaanotin on julkaistava salausavain, kutsutaan hänen julkisen avaimen.

• Joitakin vakuutus aitouden julkinen avain tarvitaan tässä järjestelmässä välttää huijaus, jonka vastustaja kuin vastaanotin. Yleensä tällainen salausjärjestelmä koskee luotettua kolmatta osapuolta, joka todistaa, että tietty julkinen avain kuuluu vain tietylle henkilölle tai yhteisölle.,

• Salaus algoritmi on monimutkainen tarpeeksi kieltää hyökkääjä alkaen liittäessään selkokielisen päässä salateksti salaus (julkinen) – näppäintä.

• Vaikka yksityiset ja julkiset avaimet liittyvät toisiinsa matemaattisesti, se ei ole mahdollista laskea yksityinen avain julkisen avaimen. Itse asiassa, älykäs osa tahansa julkisen avaimen cryptosystem on suunnittelussa suhde kahden avaimen.

julkisen avaimen salausjärjestelmiä on kolmenlaisia., Meidän keskustella niistä seuraavat osat −

RSA-Kryptosysteemi

Tämä kryptosysteemi on yksi alkuperäisen järjestelmän. Se on edelleen eniten käytetty cryptosystem vielä tänään. Järjestelmän keksivät kolme tutkijaa Ron Rivest, Adi Shamir ja Len Adleman, ja siksi sitä kutsutaan nimellä RSA cryptosystem.

Saamme nähdä kaksi puolta, RSA-salausjärjestelmä, ensinnäkin sukupolven avainparin ja toiseksi salaus-salauksen algoritmeja.,

Sukupolven RSA Key Pair

Jokainen ihminen tai puolue, joka haluaa osallistua viestinnän salauksen käyttäminen on luoda avainpari, eli julkinen avain ja yksityinen avain. Prosessia seurasi sukupolven avaimet on kuvattu alla −

• Luo RSA-modulus (n)

  • Valitse kaksi suuria alkulukuja, p ja q.

  • Laske n=p*q. Vahva särkymätön-salausta, anna n: n olla suuri määrä, yleensä vähintään 512 bittiä.,

• Löytää Johdettu Numero (e)

  • Numero e on oltava suurempi kuin 1 ja pienempi kuin (p − 1)(q − 1).

  • ei saa olla yhteinen tekijä e ja (p − 1)(q − 1) lukuun ottamatta 1. Toisin sanoen kaksi numeroa e ja (p – 1)(q – 1) ovat keskenään jaottomia.

• Muodostavat julkisen avaimen

  • pari numerot (n, e) muodostavat RSA julkisen avaimen, ja se on julkistettava.,

  • Mielenkiintoista, vaikka n on osa julkisen avaimen, vaikeuksia factorizing suuri alkuluku varmistaa, että hyökkääjä voi löytää rajallinen aika, kaksi primes (p & q) avulla saadaan n. Tämä on vahvuus RSA.

• Luo yksityinen avain

  • Yksityinen Avain d lasketaan p, k, ja e. Annetaan n: n ja e, on ainutlaatuinen määrä d.

  • Numero d on käänteinen e modulo (p – 1)(q – 1)., Tämä tarkoittaa, että d on useita alle (p – 1)(q – 1) siten, että kun kerrotaan e, se on yhtä kuin 1 modulo (p – 1)(q – 1).

  • Tämä suhde on kirjoitettu matemaattisesti seuraavasti −

ed = 1 mod (p − 1)(q − 1)

Laajennettu Eukleideen Algoritmi vaatii p, k, ja e, kuten tulo-ja antaa d tuotokseksi.

Esimerkki

esimerkki tuottaa RSA-avainpari on alla. (Ymmärryksen helpottamiseksi tässä otetut primes p & q ovat pieniä arvoja. Käytännössä nämä arvot ovat erittäin korkeat).,

• Let two primes be p = 7 and q = 13. Näin ollen modulus n = pq = 7 x 13 = 91.

• Valitse e = 5, joka on kelvollinen valinta, koska ei ole numero, joka on yhteinen tekijä 5 ja (p − 1)(q− 1) = 6 × 12 = 72, paitsi 1.

• pari numerot (n, e) = (91, 5) muodostaa julkinen avain ja voidaan tehdä käytettävissä kaikille, joille haluamme pystyä lähettää meille salattuja viestejä.

• Input p = 7, q = 13, ja e = 5. Laajennettu Eukleideen Algoritmi. Tuotos on D = 29.,

• Tarkista, että d on laskettu oikein laskemalla −

de = 29 × 5 = 145 = 1 mod 72

• Näin ollen julkinen avain on (91, 5) ja yksityiset avaimet on (91, 29).

Salaus ja Salauksen

Kun avainpari on luotu, prosessi-salaus ja salauksen purku ovat suhteellisen yksinkertaisia ja laskennallisesti helppoa.

mielenkiintoista on, että RSA ei toimi suoraan bittien merkkijonoilla kuten symmetrisen avaimen salauksen tapauksessa. Se toimii numeroilla modulo n. siksi on tarpeen edustaa plaintext kuin sarja numeroita alle n.,

RSA-Salaus

• Oletetaan, että lähettäjä haluaa lähettää tekstiviestin jollekin, jonka julkinen avain on (n, e).

• lähettäjän sitten edustaa selkokielisen kuin sarja numeroita vähemmän kuin n.

• salata ensimmäisen selkokielisen P, joka on numero modulo n. Salaus prosessi on yksinkertainen matemaattinen askel, koska −

C = Pe mod n

• Toisin sanoen, salateksti C on yhtä suuri kuin selkokielisen P kerrottuna itse e kertaa ja sitten vähentää modulo n. Tämä tarkoittaa, että C on myös useita vähemmän kuin n.,

• Palatakseni meidän Sukupolvi esimerkiksi selkokielisen P = 10, saamme salateksti C −

C = 105 mod 91

RSA-Salauksen

• salauksen prosessi RSA on myös hyvin suoraviivainen. Oletetaan, että vastaanotin julkinen avainpari (n, e) on saanut salateksti C.

• Vastaanotin nostaa C valtaa hänen yksityinen avain d. Tulos modulo n on selkokielisen P.,

Plaintext = Cd mod n

• Palaavat taas meidän numeerinen esimerkki, salateksti C = 82 saisi purettu numero 10 käyttämällä yksityistä avainta 29 −

Plaintext = 8229 mod 91 = 10

RSA-Analyysi

turvallisuus RSA riippuu vahvuuksia kaksi erillistä toimintoa. RSA-salausjärjestelmä on suosituin julkisen avaimen salausjärjestelmä vahvuus, joka perustuu käytännön vaikeus factoring erittäin suuri määrä.,

• Salaus − Se pidetään yksisuuntainen funktio muuntaa selkokielisen osaksi salateksti ja se voidaan kääntää vain tietoa yksityisen avaimen. d.

• Key Generation − vaikeus määritettäessä yksityisen avaimen RSA julkinen avain vastaa factoring modulus n. Hyökkääjä siten voi käyttää tietoa RSA julkisen avaimen määrittää yksityinen RSA-avain, ellei hän voi tekijä n. Se on myös yksi tapa toimia, menee p & q-arvot modulus n on helppoa, mutta käänteinen ei ole mahdollista.,

Jos jompikumpi näistä kahdesta funktiosta osoittautuu ei-yksisuuntaiseksi, RSA rikkoutuu. Itse asiassa, jos tekniikka factoring tehokkaasti kehitetään niin RSA ei ole enää turvallinen.

vahvuus RSA-salaus rajusti menee alas hyökkäyksiä vastaan jos numero p ja q eivät ole suuria alkulukuja ja/ tai valitaan julkinen avain e on pieni määrä.

ElGamal Cryptosystem

yhdessä RSA: n kanssa on ehdotettu muitakin julkisen avaimen salausjärjestelmiä. Monet niistä perustuvat diskreetin logaritmin ongelman eri versioihin.,

kryptosysteemi ElGamal, nimeltään Elliptinen Käyrä-Variantti, joka perustuu Diskreetin Logaritmin Ongelmaan. Se saa voimaa siitä olettamuksesta, että diskreettien logaritmien ei löydy käytännön ajassa tietty määrä, kun taas käänteinen toiminta virta voidaan laskea tehokkaasti.

Anna meidän mennä läpi yksinkertainen versio ElGamal, joka toimii numeroiden modulo p. Tapauksessa elliptinen käyrä variantteja, se perustuu aivan eri numero järjestelmiä.,

Sukupolven ElGamal Avain Pair

Jokainen käyttäjä kryptosysteemi ElGamal luo avainparin kautta seuraavasti.

• Valitsemalla suuri alkuluku p. Yleensä alkuluku 1024 2048 bittiä pituus on valittu.

• Valitseminen generaattori elementti g.

  • Tämä numero on välillä 1 ja p − 1, mutta voi olla mikä tahansa numero.

  • Se on generaattori multiplicative ryhmä kokonaislukuja modulo p. Tämä tarkoittaa, että jokainen kokonaisluku m co-prime p, on olemassa kokonaisluku k siten, että gk=a mod n.,

    esimerkiksi 3 on ryhmän 5 Generaattori (Z5 = {1, 2, 3, 4}).

N	3n	3n mod 5
1	3	3
2	9	4
3	27	2
4	81	1

• Valitsemalla oma avain. Private key x on mikä tahansa luku suurempi kuin 1 ja pienempi kuin p−1.

• Computing part of the public key., Arvo y on laskea parametrit p -, g-ja yksityinen avain x seuraavasti −

y = gx mod p

• Saada Julkisen avaimen. ElGamal public key koostuu kolmesta muuttujasta (p, g, y).

  esimerkiksi oletetaan, että p = 17 ja että g = 6 (voidaan vahvistaa, että 6 on ryhmän Z17 generaattori). Yksityinen avain x voi olla mikä tahansa numero suurempi kuin 1 ja pienempi kuin 71, joten valitsemme x = 5. Arvo y on sitten laskettu seuraavasti −

y = 65 mod 17 = 7

• Siten, että yksityinen avain on 62 ja julkinen avain on (17, 6, 7).,

Salaus ja Salauksen

sukupolven ElGamal avain pari on suhteellisen yksinkertaisempi kuin vastaava prosessi RSA. Salaus ja salauksen purku ovat kuitenkin hieman RSA: ta monimutkaisempia.

ElGamal Salaus

Oletetaan, että lähettäjä haluaa lähettää selväkielisenä jollekin, jonka ElGamal julkinen avain on (p, g, y), sitten −

• Lähettäjän edustaa selkokielisen kuin sarja numeroita modulo p.

• salata ensimmäisen selkokielisen P, jossa on edustettuina useita modulo p., Salaus saadaan salateksti C on seuraava −

  • Satunnaisesti tuottaa useita k;
  • Laske kaksi arvoa C1 ja C2, jossa −

C1 = gk mod pC2 = (P*yk) mod p

• Lähetä salateksti C, joka koostuu kaksi erillistä arvot (C1, C2), lähetetään yhdessä.,

• Viitaten meidän ElGamal avain sukupolvi yllä annettu esimerkki, selkokielisen P = 13 salataan, kun seuraa −

  • Satunnaisesti tuottaa useita, sanovat, k = 10
  • Laske kaksi arvoa C1 ja C2, jossa −

C1 = 610 mod 17C2 = (13*710) mod 17 = 9

• Lähetä salateksti C = (C1, C2) = (15, 9).,

ElGamal Salauksen

• purkaa salatekstin (C1, C2) käyttäen yksityinen avain, x, seuraavat kaksi askelta on otettu, −

  • Laske modulaarinen käänteinen (C1)x modulo p, joka on (C1)-x , kutsutaan yleisesti salauksen tekijä.,

  • Saada selkokielisen käyttämällä seuraavaa kaavaa −

C2 × (C1)-x mod p = Plaintext

• Tässä esimerkissä, purkaa salateksti C = (C1, C2) = (15, 9) käyttäen yksityinen avain, x = 5, salauksen tekijä on se,

15-5 mod 17 = 9

• Pura selkokielisen P = (9 × 9) mod 17 = 13.

ElGamal-Analyysi

ElGamal-järjestelmä, jokaisella käyttäjällä on oma avain x. ja on kolme osatekijää julkinen avain − prime modulus p, generaattori g, ja julkisen Y = gx mod p., Elgamalin vahvuus perustuu diskreetin logaritmiongelman vaikeuteen.

secure key koko on yleensä > 1024 bittiä. Nykyään jopa 2048 bittiä pitkä avain käytetään. Käsittelynopeusrintamalla Elgamal on melko hidas, sitä käytetään pääasiassa avaintodennusprotokolliin. Koska suurempi käsittelyn tehokkuutta, Ellipsinmuotoinen Käyrä variantteja ElGamal ovat yhä suositumpia.,

Elliptinen Käyrä Salaus (ECC)

Elliptinen Käyrä Salaus (ECC) on termi, jota käytetään kuvaamaan suite salauksen työkaluja ja protokollia, joiden turvallisuus perustuu erityisiä versioita diskreetin logaritmin ongelma. Se ei käytä numeroita modulo p.

ECC perustuu sarjaa numeroita, jotka liittyvät matemaattisia objekteja kutsutaan ellipsinmuotoinen käyriä. On sääntöjä lisäämällä ja laskemalla kerrannaisia näistä numeroista, aivan kuten on numerot modulo p.,

ECC sisältää muunnelmia monet cryptographic järjestelmiä, jotka on alun perin suunniteltu modulaarinen numerot kuten ElGamal salaus ja Digitaalinen Allekirjoitus-Algoritmi.

diskreetin logaritmiongelman uskotaan olevan paljon vaikeampi, kun sitä sovelletaan elliptisellä käyrällä oleviin pisteisiin. Tämä edellyttää siirtymistä numeroista modulo p ellipsimäisen käyrän pisteisiin. Myös vastaava turvataso voidaan saada lyhyemmillä näppäimillä, jos käytämme ellipsinmuotoisia käyräpohjaisia variantteja.,

lyhyempi avaimet johtaa kaksi etua −

• Helppo avainten hallinta
• Tehokas laskenta

Nämä edut tehdä elliptinen-käyrän-pohjainen variantteja salaus järjestelmä on erittäin houkutteleva sovellus, jossa tietojenkäsittelyn resurssit ovat rajoitetut.

RSA-ja ElGamal Järjestelmät – Vertailu

olkaamme lyhyesti vertailla RSA-ja ElGamal järjestelmiä eri näkökohtia.

RSA	ElGamal
Se on tehokkaampaa salausta.	se on tehokkaampi salauksen purkamiseen.,
Se on vähemmän tehokas salauksen.	se on tehokkaampi salauksen purkamiseen.
tietyn turvatason osalta RSA: ssa vaaditaan pitkiä avaimia.	saman turvallisuustason osalta vaaditaan hyvin lyhyitä avaimia.
Se on laajalti hyväksytty ja käytetty.	se on uusi eikä kovin suosittu markkinoilla.