Vertailevaa Tutkimusta: Etsivät Suhteita Muuttujien
toisin kuin kuvaileva tutkimus, jonka tarkoituksena on ensisijaisesti tarjota staattisia kuvia, vertailevaa tutkimusta liittyy mittauksen kahden tai useamman relevantit muuttujat ja arvioinnin suhdetta tai niistä muuttujia., Esimerkiksi pituuden ja painon muuttujat liittyvät systemaattisesti toisiinsa (korreloivat), koska pidemmät ihmiset painavat yleensä enemmän kuin lyhyemmät ihmiset. Samalla tavalla, tutkimuksen aika ja muistin virheet liittyvät myös, koska enemmän aikaa henkilö on antanut tutkia listan sanoja, vähemmän virheitä hän tekee. Kun tutkimussuunnittelussa on kaksi muuttujaa, toista niistä kutsutaan prediktorimuuttujaksi ja toista tulosmuuttujaksi., Tutkimuksen suunnittelu voidaan visualisoida, kuten tämä, jossa kaareva nuoli edustaa odotettavissa korrelaatio näiden kahden muuttujan välillä:
Kuva 2.2.2

Yksi tapa järjestää tietoja vertailevaa tutkimusta, jossa on kaksi muuttujat on kuvaajan arvot jokaisen mitattujen muuttujien avulla scatter tontti. Kuten kuvasta 2.10 näkyy ”esimerkkejä Scatter-tonteista”, scatter-juoni on visuaalinen kuva kahden muuttujan suhteesta., Piste piirretään kullekin yksilölle kahden muuttujan pistemäärien leikkauspisteessä. Kun yhdistys muuttujien välillä on scatter tontti voidaan helposti approksimoida suoraan, kuten osissa (a) ja (b) Kuva 2.10 ”Esimerkkejä sirontakuvaajiin”, muuttujien sanotaan olevan lineaarinen suhde.
Kun suora linja osoittaa, että henkilöt, jotka ovat keskimääräistä arvot yksi muuttuja on myös yleensä keskimääräistä arvoja toinen muuttuja, kuten osa (a), suhde on sanottu olevan positiivinen lineaarinen., Esimerkkejä positiivisista lineaarisista suhteista ovat pituuden ja painon, koulutuksen ja tulojen sekä lasten iän ja matemaattisten kykyjen väliset suhteet. Joka tapauksessa ihmiset, jotka pisteet korkeampi yksi muuttujista myös yleensä pisteet korkeampi toisen muuttujan. Negatiivinen lineaarinen suhteita, sen sijaan, kuten on esitetty osa (b), esiintyä, kun edellä keskimääräiset arvot yhden muuttujan liittyy yleensä keskimääräistä arvoja toinen muuttuja., Esimerkkejä negatiivinen lineaarinen suhteita ovat ne, välillä lapsen ikä ja määrä vaippoja lapsi käyttää, ja välillä harjoitella ja virheitä tehdään oppimisen tehtävä. Näissä tapauksissa ihmiset, jotka pisteet korkeampi yksi muuttujista yleensä Pisteet alempi toinen muuttuja.
muuttujien väliset Suhteet, joita ei voida kuvata suoralla viivalla tunnetaan epälineaarinen suhteita. Kuvan 2.10 ”esimerkkejä Scatter-tonteista” osassa (c) on yhteinen kuvio, jossa pisteiden jakautuminen on pääosin satunnaista., Tällöin näiden kahden muuttujan välillä ei ole minkäänlaista suhdetta, ja niiden sanotaan olevan riippumattomia. Osat (d) ja (e) Kuva 2.10 ”Esimerkkejä sirontakuvaajiin” näytä malleja yhdistys, joka, vaikka on yhdistys, pisteitä ei hyvin kuvata yhdellä suora viiva. Esimerkiksi osassa (d) esitetään, millainen suhde ahdistuksen ja suorituksen välillä usein esiintyy., Lisää ahdistusta alhaisesta kohtalainen arvot liittyvät suorituskyky kasvaa, kun taas lisää ahdistusta kohtalaisen korkea arvot liittyvät laskee suorituskykyä. Ihmissuhteita, jotka muuttuvat suuntaan ja joita ei siten kuvata yhdellä suoralla, kutsutaan kurvikkaiksi ihmissuhteiksi.
Kuva 2.10 Esimerkkejä Scatter Tonttien
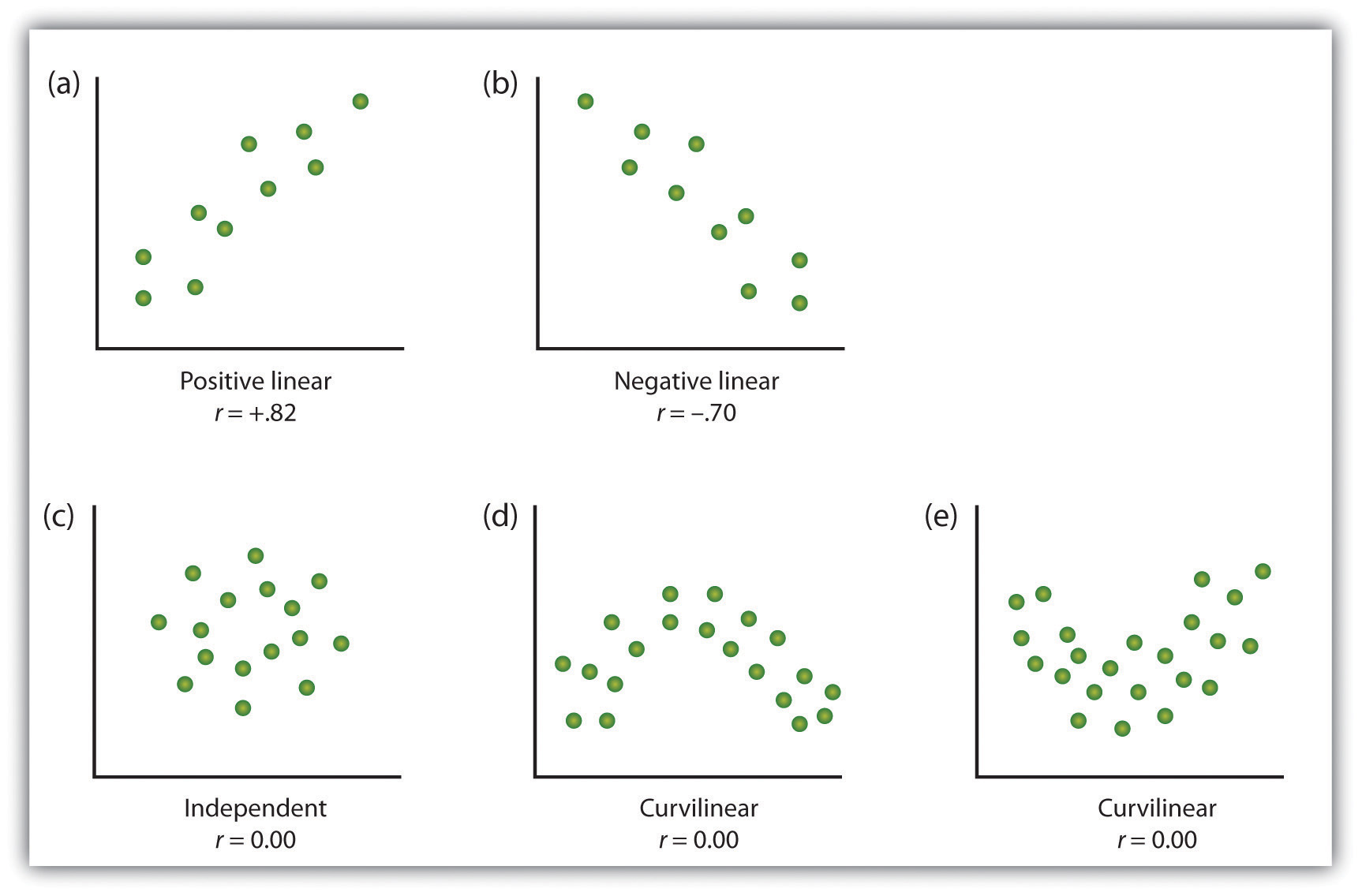
esimerkkejä suhteita kaksi muuttujaa, kuten on esitetty sirontakuvaajiin., Huomaa, että Pearsonin korrelaatiokerroin (r) muuttujien välillä on kaareva suhteita on todennäköisesti lähellä nollaa.
sovitettu stangorista, C. (2011). Käyttäytymistieteiden tutkimusmenetelmät (4. ed.). Vuoristomaisema, CA: Cengage.
yleisin tilastollinen mitta vahvuus lineaarisia suhteita muuttujien Pearsonin korrelaatiokerroin, joka symboloi r-kirjain. Arvo korrelaatiokerroin vaihtelee välillä r = -1.00 r = +1.00., Lineaarisen suhteen suunta ilmoitetaan korrelaatiokertoimen merkillä. R: n positiiviset arvot (kuten r = .54 tai r = .67) osoittavat, että suhde on positiivinen lineaarinen (eli kuvion pisteet scatter tontti alkaa vasemmalla alhaalla oikeassa yläkulmassa), kun taas negatiiviset arvot r (kuten r = –.30 tai r = –.72) ilmaise negatiiviset lineaariset suhteet (eli pisteet kulkevat ylavasemmalta oikealle). Lineaarisen suhteen voimakkuus indeksoidaan korrelaatiokertoimen etäisyydellä nollasta (sen itseisarvo)., Esimerkiksi r = –.54 on vahvempi suhde kuin r = .30, ja r = .72 on vahvempi suhde kuin r = –.57. Koska Pearsonin korrelaatiokerroin mittaa vain lineaarista suhteita, muuttujia, jotka ovat kaareva suhteet eivät ole hyvin kuvattu r, ja havaittu korrelaatio on lähellä nollaa.
on myös mahdollista tutkia suhteita yli kahden toimenpiteen kesken samanaikaisesti., Tutkimuksen suunnittelu, jossa useampi kuin yksi ennustaja muuttuja on käyttää ennustamaan yhden tuloksen muuttuja on analysoitu läpi useita regressio (Aiken & West, 1991). Useita regressio on tilastollinen tekniikka, joka perustuu korrelaatiokertoimet muuttujien joukossa, jonka avulla ennustaa yhden tulos vaihtelee enemmän kuin yksi ennustaja muuttuja. Esimerkiksi, Kuva 2.11 ”Ennustus työsuorituksen Kolme Ennustaja Muuttujat” osoittaa, useita regressioanalyysi, jossa kolme ennustaja muuttujat ovat käyttää ennustamaan yhden tuloksen., Käyttää useita regressioanalyysi osoittaa, tärkeä etu vertailevaa tutkimusta malleja—ne voidaan tehdä ennusteita siitä, henkilö on todennäköisesti pisteet tulos muuttuja (esim., job performance), joka perustuu tiedon muihin muuttujiin.
Kuva 2.11 Ennuste työsuorituksen Kolme Ennustaja Muuttujat
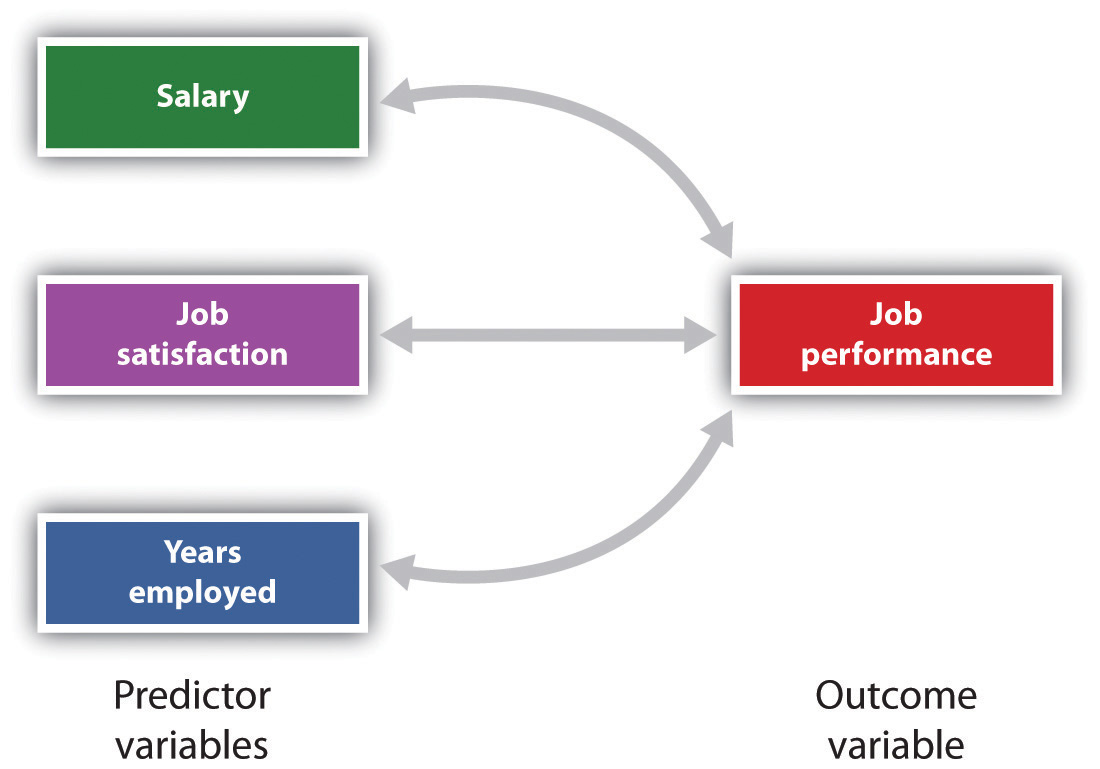
Multiple regression avulla tutkijat voivat ennustaa tulokset yhdellä tulos muuttuja käyttäen enemmän kuin yksi ennustaja muuttuja.,
tärkeä rajoitus vertailevaa tutkimusta malleja on, että niiden perusteella ei voida tehdä johtopäätöksiä syy-seuraussuhteita niistä mitataan muuttujia. Ajatellaanpa esimerkiksi erästä tutkijaa, joka on olettanut, että väkivaltaisen käytöksen katsominen lisää aggressiivista leikkiä lapsilla. Hän on kerännyt, mistä näyte neljännen luokan lasten, mitata, kuinka paljon väkivaltaisia televisio-ohjelmia kunkin lapsen näkemyksiä viikon aikana, sekä mitata, kuinka aggressiivisesti jokainen lapsi soittaa koulun pihalla., Kerätyistä tiedoistaan tutkija löytää positiivisen korrelaation kahden mitatun muuttujan välillä.
Vaikka tämä positiivinen korrelaatio näyttää tukevan tutkijan hypoteesi, sitä ei voida pitää merkkinä siitä, että katselu väkivaltaisten televisio aiheuttaa aggressiivista käyttäytymistä. Vaikka tutkija on taipuvainen olettaa, että katselu väkivaltaisten televisio aiheuttaa aggressiivinen pelata,
Kuva 2.2.2

on olemassa muita mahdollisuuksia., Yksi vaihtoehtoinen mahdollisuus on, että syy-suunta on juuri päinvastainen kuin mitä on arveltu. Ehkä lapset, jotka ovat käyttäytyneet aggressiivisesti koulussa kehittää jäljellä jännitystä, joka johtaa heidät haluavat katsella väkivaltaisia tv-ohjelmia kotona:
Kuva 2.2.2

Vaikka tämä mahdollisuus voi tuntua vähemmän todennäköistä, ei ole mitään keinoa sulkea pois mahdollisuutta, että tällainen käänteinen syy tämän perusteella havaittu korrelaatiota., On myös mahdollista, että sekä syy-ohjeet ovat toimivia ja, että kahden muuttujan aiheuttaa toisilleen:
Kuva 2.2.2

Vielä yksi mahdollinen selitys sille, että havaittu korrelaatio on, että se on tuotettu läsnäolo yhteinen-syy-muuttuja (tunnetaan myös nimellä kolmas muuttuja)., Yhteinen-syy-muuttuja on muuttuja, joka ei ole osa tutkimuksen hypoteesi, mutta se aiheuttaa sekä ennustaja ja tulos muuttuja ja siten tuottaa havaittu korrelaatio niiden välillä. Esimerkissämme mahdollinen yleinen-Kausaalinen muuttuja on lasten vanhempien kuritustyyli. Vanhemmat, jotka käyttävät ankara ja rankaiseva kurinalaisuutta tyyli voi tuottaa lapsia, jotka molemmat haluavat katsella väkivaltaisia tv-ja jotka käyttäytyvät aggressiivisesti verrattuna lapsiin, joiden vanhemmat käyttävät vähemmän ankara kuri:
Kuva 2.2.,2
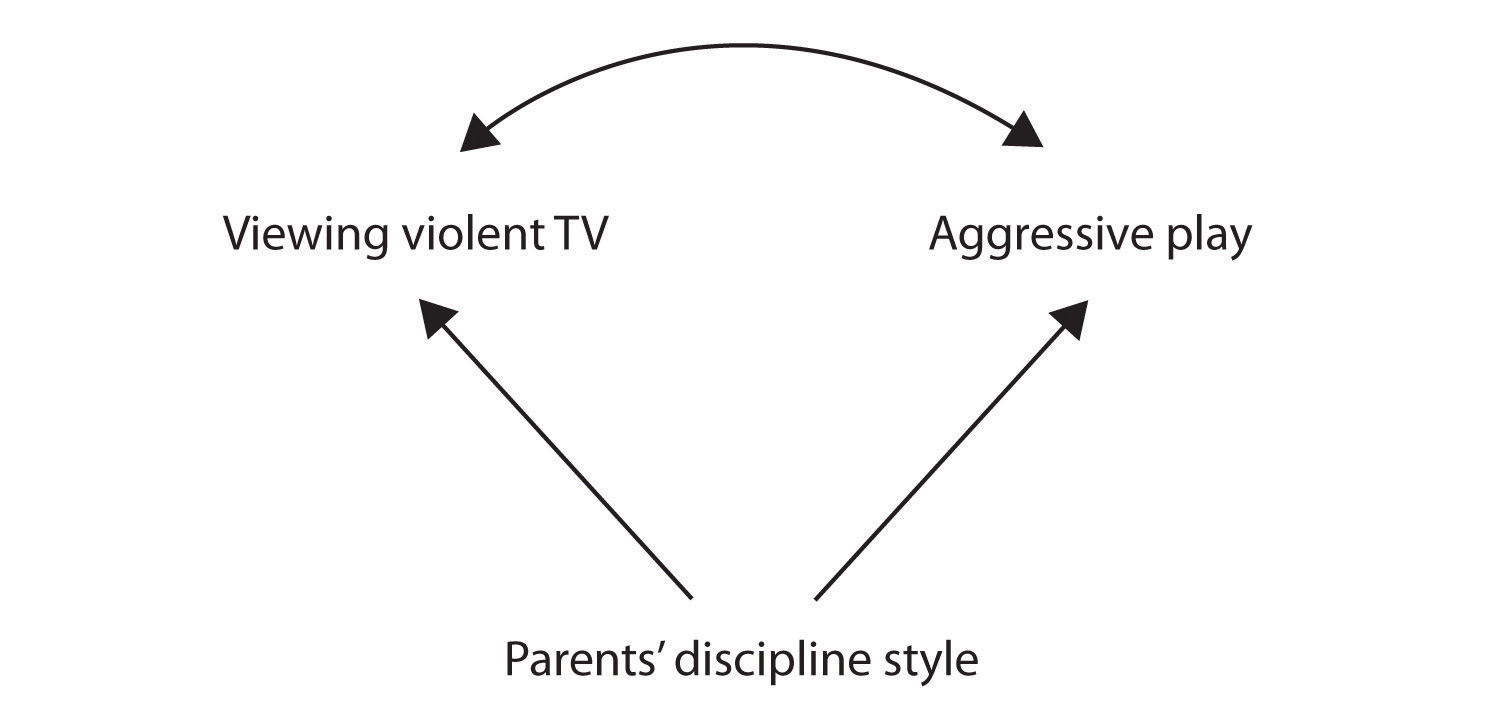
tässä tapauksessa, television katselu ja aggressiivinen peli olisi korreloi positiivisesti (kuten kaareva nuoli välillä), vaikka kumpikaan ei aiheuttanut muita, mutta he olivat molemmat aiheuttama kurinalaisuutta tyyli vanhemmat (suora nuolet). Kun ennustaja ja tulosmuuttujat ovat molemmat aiheuttama yhteinen-syy-muuttujan havaittu suhde niiden välillä on sanottu olevan vääriä., Väärä suhde on suhde kaksi muuttujaa, joiden yhteinen-syy-muuttuja tuottaa ja ”selittää pois” suhde. Jos vaikutuksia yhteisestä syy-muuttuja otettiin pois, tai ohjattu, suhde ennustaja ja tulosmuuttujat katoaisi. Esimerkiksi suhde aggressiivisuutta ja television katselu saattaa olla väärä, koska kontrolloimalla vaikutus vanhempien kurittaminen tyyli, suhdetta television katseluun ja aggressiivinen käyttäytyminen saattaa mennä pois.,
Common-syy-muuttujien korrelaatiota tutkimuksen malleja voi olla ajatellut kuin ”mysteeri” muuttujia, koska niitä ei ole mitattu, niiden läsnäolo ja identiteetti ovat yleensä tuntematon tutkija. Koska se ei ole mahdollista mitata jokaisen muuttuja, joka voi aiheuttaa sekä ennustaja ja tulosmuuttujat, olemassaolon tuntematon yleinen-syy-muuttuja on aina mahdollisuus. Tästä syystä meille jää perus rajoitus vertailevaa tutkimusta: Korrelaatio ei osoita syy-yhteyttä., On tärkeää, että kun olet lukenut vertailevaa tutkimushanketta, pitää mielessä mahdollisuus näennäisiä suhteita, ja olla varma, tulkita löydökset oikein. Vaikka vertailevaa tutkimusta on joskus raportoitu osoittaa syy-yhteyttä ilman mitään mainintaa mahdollisuus kääntää syy-yhteys tai yhteinen-syy-muuttujia, valistuneet kuluttajat tutkimusta, kuten sinä, ovat tietoisia näistä interpretational ongelmia.
summa, korrelaatio tutkimus malleja on sekä vahvuuksia ja rajoituksia., Yksi vahvuus on, että niitä voidaan käyttää, kun kokeellinen tutkimus ei ole mahdollista, koska ennustaja muuttujat voi olla manipuloitu. Korrelaatiomalleilla on myös se etu, että tutkija voi tutkia käyttäytymistä sellaisena kuin sitä esiintyy arjessa. Ja voimme myös käyttää korrelaatiota malleja tehdä ennusteita—esimerkiksi ennustaa, tulokset niiden akku testien onnistumista työn harjoittelijoihin harjoittelun aikana. Mutta emme voi käyttää tällaista vertailevaa tietoa onko koulutus aiheutti parempi työsuoritus. Siihen tutkijat luottavat kokeissa.,