Imaginaariluvut

imaginaariluku potenssiin laskettuna antaa negatiivisen tuloksen.

Kokeile

yritetään neliöimistä jotkut numerot nähdä, jos voimme saada negatiivinen tulos:

Ei onnea! Aina positiivinen, tai nolla.

vaikuttaa siltä, että emme voi kertoa numeroa itsestään saadaksemme negatiivisen vastauksen …,

… mutta kuvitella, että siellä on tällainen numero (kutsuvat sitä en kuvitteellinen), joka voi tehdä tämän: i × i = -1 – se Olisi hyödyllinen, ja mitä voimme tehdä sen kanssa?

No, ottamalla neliöjuuri molemmilta puolilta saamme tämän:

Mikä tarkoittaa, että minulla on vastaus neliöjuuri -1.

joka on itse asiassa erittäin hyödyllinen, koska …

Anna meidän mennä:

Hei! se oli mielenkiintoista! Neliöjuuri -9 on yksinkertaisesti neliöjuuri +9, kertaa minä.,

yleistä:

Niin kauan kuin meillä on tuo pieni ”i” on muistuttaa meitä siitä, että meillä on vielä
täytyy kerrotaan √-1 olemme turvallista jatkaa meidän ratkaisu!

I

Mielenkiintoinen! Käytimme kuvitteellista lukua (5i) ja päädyimme todelliseen ratkaisuun (-25).,

Kuvitteellinen numerot voivat auttaa meitä ratkaisemaan joitakin yhtälöt:

Yksikkö Kuvitteellinen Numero

neliöjuuri miinus yksi √(-1) on ”yksikkö” Kuvitteellinen Numero, vastaa 1 Real Numerot.

matematiikassa √(-1) symboli on I imaginaarille.

voitko ottaa neliöjuuren -1?
Well I can!

mutta elektroniikassa he käyttävät j: tä (koska ”i” tarkoittaa jo nykyistä, ja seuraava kirjain I: n jälkeen on j).,

Examples of Imaginary Numbers

Imaginary Numbers are not ”Imaginary”

Imaginary Numbers were once thought to be impossible, and so they were called ”Imaginary” (to make fun of them).,

Mutta sitten ihmiset tutkinut niitä lisää ja selvisi, että ne olivat todella hyödyllisiä ja tärkeitä, koska ne täyttää aukon matematiikka … ”kuvitteellinen” nimi on kuitenkin jäänyt jumiin.

ja näin syntyi myös nimi ”reaaliluvut” (real ei ole kuvitteellinen).,

Kuvitteellinen Numerot ovat Hyödyllisiä

Monimutkainen Numerot

Kuvitteellinen numeroita on tullut eniten hyötyä, kun se yhdistetään todellinen määrä tehdä monimutkaisia numeroita, kuten 3+5i−tai 6-4i

Spectrum Analyzer

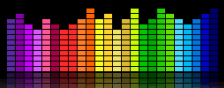
Niille viileä näyttää näet, kun musiikki soi? Jep, monimutkaisia numeroita käytetään laskemaan niitä! Käyttämällä jotain nimeltä ”Fourier Transforms”.,

itse asiassa monet nokkelat asiat voidaan tehdä äänellä kompleksilukujen avulla, kuten suodattamalla ääniä, kuulemalla kuiskauksia väkijoukossa ja niin edelleen.

se kuuluu ”signaalinkäsittely” – nimiseen aiheeseen.

Sähkön

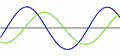
AC (Vaihtovirta) Sähkö muuttuu positiivisen ja negatiivisen välillä on siniaalto.

kun yhdistämme kaksi vaihtovirtaa, ne eivät välttämättä täsmää kunnolla, ja uuden virran selvittäminen voi olla hyvin vaikeaa.,

mutta kompleksilukujen käyttäminen helpottaa laskelmien tekemistä.

ja tuloksessa voi olla ”kuvitteellinen” virta, mutta se voi silti satuttaa sinua!

Mandelbrot Set

kaunis Mandelbrot Set (osa kuvassa) perustuu Monimutkaisia Numeroita.,

toisen Asteen Yhtälö

toisen Asteen Yhtälö, jolla on monia käyttötarkoituksia,
voi antaa tuloksia, jotka sisältävät kuvitteellinen numerot

Myös Tieteen, kvanttimekaniikka ja Suhteellisuusteoria käyttää monimutkaisia numeroita.

mielenkiintoinen ominaisuus

yksikön kuvitteellinen Numero, i, on mielenkiintoinen ominaisuus., It ”cycles” through 4 different values each time we multiply:

1 × i = i i × i = −1 −1 × i = −i −i × i = 1 Back to 1 again!,

So we have this: