Sovellukset Pascalin Periaate ja Hydrauliset Järjestelmät
Me voimme saada suhdetta voimia tässä yksinkertainen hydraulinen järjestelmä soveltamalla Pascalin periaate. Huomaa ensin, että järjestelmän kaksi mäntää ovat samalla korkeudella, joten paineessa ei ole eroa syvyyserosta johtuen. Paine johtuu F1 toimii alueella A1 on yksinkertaisesti
\(p_{1} = \frac{F_{1}}{A_{1}}\), sellaisena kuin se määritellään \(p = \frac{F}{A}\).,
\
Tämä yhtälö liittyy suhdeluvut voima-alueen kaikki hydraulinen järjestelmä, edellyttäen, että männät ovat samaan pystysuora korkeus, ja että kitka järjestelmässä on vähäinen.
Hydrauliset järjestelmät voivat lisätä tai vähentää voimaa soveltaa niitä. Jotta voima olisi suurempi, paine kohdistetaan suuremmalle alueelle. Esimerkiksi jos Kuvassa 14.16 olevaan vasempaan sylinteriin kohdistetaan 100-N voima ja oikean sylinterin pinta-ala on viisi kertaa suurempi, lähtövoima on 500 N., Hydrauliset järjestelmät ovat analogisia yksinkertaisten vipujen kanssa, mutta niillä on se etu, että paine voidaan lähettää kiduttavan kaarevien linjojen kautta useisiin paikkoihin kerralla.
hydraulinen tunkki on tällainen hydraulinen järjestelmä. Hydraulisella tunkilla nostetaan raskaita kuormia, esimerkiksi automekaanikkojen käyttämiä autoja. Se koostuu U-putkessa olevasta epätäydellisestä nesteestä, jossa on liikuteltava mäntä kummallakin puolella. U-putken toinen puoli on kapeampi kuin toinen., Pienellä alueella kohdistettu pieni voima voi tasapainottaa paljon suuremman voiman toisella puolella suuremmalla alueella (Kuva \(\PageIndex{3}\)).
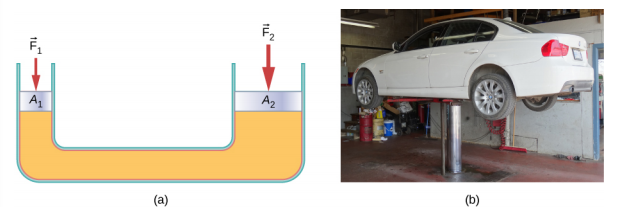
Pascalin periaatetta, se voi olla osoittaneet, että voimaa, joka tarvitaan nostamaan auto on vähemmän kuin auton painon:
\
missä F1 on voima nostaa auton, A1 on poikkipinta-ala on pienempi männän, A2 on poikkileikkauksen pinta-ala suurempi mäntä, ja F2 on auton painon.
Harjoitus \(\PageIndex{1}\)
Olisi hydraulinen paina vielä toimi oikein, jos kaasun sijasta käytetään nestemäistä?