Probability
Learning Objective(s)
· Define event, outcome, trial, simple event, sample space y calcula la probabilidad de que ocurra un evento.
div· * calcule la probabilidad de eventos para resultados más complejos.
div· * resuelve aplicaciones que implican probabilidades.
Introducción
la Probabilidad proporciona una medida de la probabilidad de que algo va a ocurrir., Es un número entre e incluyendo los números 0 y 1. Se puede escribir como una fracción, un decimal o un porcentaje.

Escoger los números al azar significa que no hay un orden específico en el que ellos son los elegidos. Muchos juegos usan dados o hilanderos para generar números al azar. Si entiendes cómo calcular probabilidades, puedes tomar decisiones reflexivas sobre cómo jugar estos juegos al conocer la probabilidad de varios resultados.,
Definiciones
en Primer lugar usted necesita saber algunos términos relacionados con la probabilidad. Cuando se trabaja con probabilidad, una acción aleatoria o una serie de acciones se denomina ensayo. Un resultado es el resultado de un ensayo, y un evento es una colección particular de resultados. Los eventos generalmente se describen usando una característica común de los resultados.
vamos a aplicar este lenguaje para ver cómo funcionan los Términos en la práctica. Algunos juegos requieren rodar un dado con seis lados, numerados del 1 al 6. (Dice es el plural de die.,) La siguiente tabla ilustra el uso del ensayo, resultado y evento para tal juego:
observe que una colección de resultados se pone en llaves y se separa por comas.
un evento simple es un evento con un solo resultado. Rodar un 1 sería un evento simple, porque solo hay un resultado que funciona: ¡1! Rodar más de un 5 también sería un evento simple, porque el evento incluye solo 6 como resultado válido. Un evento compuesto es un evento con más de un resultado. Por ejemplo, al rodar un dado de seis lados, rodar un número par podría ocurrir con uno de tres resultados: 2, 4 y 6.,
Cuando usted tira un dado de seis lados muchas veces, usted no debe esperar que ningún resultado suceda más a menudo que otro (asumiendo que es un dado justo). Los resultados en una situación como esta son igualmente probables. Es muy importante reconocer cuándo los resultados son igualmente probables al calcular la probabilidad. Dado que cada resultado en el ensayo de troquelado es igualmente probable, esperaría obtener cada resultado ![]() de los rollos., Es decir, que usted esperaría
de los rollos., Es decir, que usted esperaría ![]() de los rodillos 1,
de los rodillos 1, ![]() de los rodillos 2,
de los rodillos 2, ![]() de los rollos a ser 3, y así sucesivamente.
de los rollos a ser 3, y así sucesivamente.
un spinner se divide en cuatro partes iguales, cada una coloreada con un color diferente como se muestra a continuación. Cuando este hilador se hace girar, la flecha apunta a uno de los colores. Son los resultados igualmente probables?
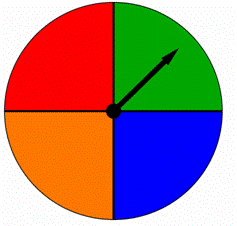
A) Sí, son igualmente probables.
B) No, No son igualmente probables.,
Probabilidad de Eventos
La probabilidad de un evento es la frecuencia con que se espera que ocurra. Es la relación entre el tamaño del espacio de eventos para el tamaño del espacio muestral.
primero, debe determinar el tamaño del espacio de muestra. El tamaño del espacio muestral es el número total de posibles resultados. Por ejemplo, al rodar 1 dado, el espacio de muestra es 1, 2, 3, 4, 5, An 6. Así que el tamaño del espacio de la muestra es 6.
luego debe determinar el tamaño del espacio para eventos., El espacio del evento es el número de resultados en el evento que le interesa. El espacio de eventos para rodar un número menor a tres es 1 o 2. Así que el tamaño del espacio para eventos es 2.
para resultados igualmente probables, la probabilidad de un evento E se puede escribir P (E).
![]()
|
Ejemplo |
||
|
Problema |
Un juego requiere un laminado de seis caras morir numeradas del 1 al 6., ¿Cuál es la probabilidad de rodar un número par? |
|
|
espacio Muestral = {1, 2, 3, 4, 5, 6}
espacio para Eventos = {2, 4, 6} |
en Primer lugar, encontrar el espacio muestral y el espacio para el evento. El espacio de muestra son todos los resultados posibles, y el espacio del evento son los resultados en el evento. En este caso, el evento es » rodar un número par.,» |
|
|
|
Ya que los resultados son igualmente probables, la probabilidad de que el evento es la proporción de espacio para eventos, y para muestra el espacio., |
|
|
Respuesta |
P(número) = |
|
es una práctica común con probabilidades, como con fracciones en general, para simplificar una probabilidad en términos mínimos, ya que hace que sea más fácil para la mayoría de la gente para tener una idea de lo grande que es. A menos que haya razones para no hacerlo, exprese todas las probabilidades finales en términos más bajos.,
un spinner se divide en partes iguales, cada una coloreada con un color diferente como se muestra a continuación., Encuentra la probabilidad de girar azul o verde en este spinner:
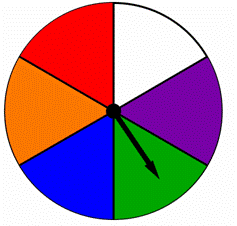
A) ![]()
B) ![]()
c) 2
d) 6
métodos de conteo para encontrar espacios de muestra
Lo más difícil para calcular una probabilidad puede ser encontrar el tamaño del espacio de muestra, especialmente si hay dos o más ensayos. Hay varios métodos de conteo que pueden ayudar.,
el PRIMERO en mirar es hacer un gráfico. En el siguiente ejemplo, Tori está volteando dos monedas. Por lo tanto, debe determinar cuidadosamente el espacio de la muestra. Un gráfico como el que se muestra en el ejemplo que sigue es un buen enfoque.
|
Ejemplo |
||||
|
Problema |
Tori es voltear un par de monedas y notar cómo muchos de los lanzamientos de «jefes» que recibe. ¿Cuál es la probabilidad de que ella Voltee 2 cabezas?, ¿Cuál es la probabilidad de que ella Voltee solo 1 cabeza?,15ecf6″>T |
T |
TT |
|
sample space: {HH, HT, TH, TT}
event space for 2 heads: {HH}
event space for 1 head: {HT, TH}
Create a chart to record the results of flipping the first coin, followed by the result of flipping the second coin.,
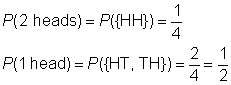
Ya que los resultados son igualmente probables, la probabilidad de que el evento es la proporción de espacio para eventos, y para muestra el espacio.,
Respuesta
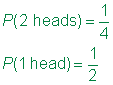
En el siguiente ejemplo, el espacio muestral para Tori es simple, ya que sólo una mueren se está implementando. Sin embargo, ya que James está rodando dos dados, un gráfico ayuda a organizar la información.,
|
Ejemplo |
||||||||
|
Problema |
Tori rodar una de seis caras morir y quería conseguir un resultado de 1 o 4. James lanzó dos dados de seis lados, uno azul y uno rojo, y quería obtener un resultado de un 1 y un 3, al mismo tiempo. ¿Qué evento tiene mayor probabilidad?, |
|||||||
|
Tori’s sample space: {1, 2, 3, 4, 5, 6}
Tori’s event space: {1, 4}
Tori:
|
First, find the sample space and the event space for the two trials., Para el juicio de Tori, esto es sencillo. dado que los resultados son igualmente probables, la probabilidad del evento es la relación entre el espacio del evento y el espacio de la muestra.,316594724″> 6 |
6,1 |
6,2 |
6,3 |
6,4 |
6,5 |
6,6 |
|
James’ sample space has 36 outcomes.,
el espacio para eventos de James tiene 2 resultados.
no es tan obvio para el juicio de James, ya que está lanzando dos dados. Utilice un gráfico para encontrar las posibilidades.
Hay 36 resultados. De estos, hay 2 que tienen 1 y 3.,
James: ![]()
Ya que los resultados son igualmente probables, la probabilidad de que el evento es la proporción de espacio para eventos, y para muestra el espacio.
Respuesta
Tori evento tiene una probabilidad mayor.,
también puede utilizar un diagrama de árbol para determinar el espacio muestral. Un diagrama de árbol tiene una rama para cada resultado posible para cada evento.
supongamos que un armario tiene tres pares de pantalones (negro, blanco y verde), cuatro camisas (verde, blanco, morado y amarillo) y dos pares de zapatos (blanco y negro). ¿Cuántos trajes diferentes se pueden hacer? Hay 3 opciones para pantalones, 4 opciones para camisas y 2 opciones para zapatos., Para nuestro diagrama de árbol, usemos B Para Negro, W para blanco, G para Verde, P Para púrpura e y para amarillo.
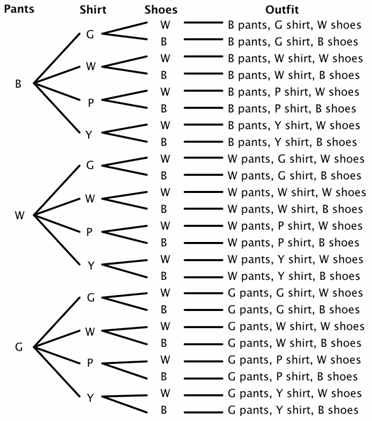
puede ver en el diagrama de árbol que hay 24 conjuntos posibles (algunas quizás no son buenas opciones) en el espacio de muestra.
ahora puede resolver fácilmente algunos problemas de probabilidad. Por ejemplo, ¿cuál es la probabilidad de que si cierras los ojos y elegir al azar se elige pantalones y zapatos del mismo color? Puedes ver que hay 8 trajes donde los pantalones y los zapatos coinciden.,
![]()
como Ha Visto, cuando un ensayo involucra más de un elemento aleatorio, como voltear más de una moneda o rodar más de un dado, no siempre es necesario identificar todos los resultados en el espacio de muestra para calcular una probabilidad. Solo necesitas el número de resultados.
el principio fundamental de conteo es una forma de encontrar el número de resultados sin enumerar y contar cada uno de ellos.,
el principio fundamental de conteo
si un evento tiene P posibles resultados, y otro evento tiene m posibles resultados, entonces hay un total de P * M posibles resultados para los dos eventos.
ejemplos
div· * rodando dos dados de seis lados: cada dado tiene 6 resultados igualmente probables, por lo que el espacio de muestra es 6 • 6 o 36 resultados igualmente probables.
* voltear tres monedas: cada moneda tiene 2 resultados igualmente probables, por lo que el espacio de muestra es 2 • 2 • 2 U 8 resultados igualmente probables.,
div· * rodar un dado de seis lados y voltear una moneda: el espacio de muestra es 6 * 2 o 12 resultados igualmente probables.
así que puedes usar el principio de conteo Fundamental para averiguar cuántos atuendos hay en el ejemplo anterior. Hay 3 opciones para pantalones, 4 opciones para camisas y 2 opciones para zapatos. Usando el principio fundamental de contar, usted tiene 4 • 3 • 2 = 24 trajes diferentes.,
|
Ejemplo |
||
|
Problema |
Barry voluntarios en una organización de caridad a pie para hacer almuerzos para todos los otros voluntarios. En cada bolsa pone: · uno de los dos sándwiches (mantequilla de maní y gelatina, o pavo y queso), · una de las tres papas (papas fritas regulares, papas fritas al horno o papas fritas de maíz), · de frutas (una manzana o una naranja)., se olvidó de marcar lo que había en las bolsas. Suponiendo que cada elección es igualmente probable, ¿Cuál es la probabilidad de que la bolsa que Therese obtiene tenga un sándwich de mantequilla de maní y jalea y una manzana?, |
|
|
Size of sample space:
(number of sandwich choices) • (number of chip choices) • (number of fruit choices) = 2 • 3 • 2 = 12
|
First, use the Fundamental Counting Principle to find the size of the sample space., |
|
|
Tamaño de espacio para eventos:
(número de opciones de sándwich en el evento) • (número de chip de decisiones en el evento) • (número de frutos opciones en el evento) = |
Por el de espacio para eventos, siguen el mismo principio. En este caso, solo hay un sándwich y una pieza de fruta de interés, pero cualquiera de los tres tipos de chips son aceptables., |
|
|
Respuesta |
|
el Uso de la relación para encontrar la probabilidad. |
Carrie voltea cuatro monedas y cuenta el número de colas. Hay cuatro maneras de conseguir exactamente una cola: HHHT, HHTH, HTHH, y THHH. ¿Cuál es la probabilidad de que Carrie reciba exactamente una cola?,
A) ![]()
B) ![]()
C) ![]()
D) ![]()
Summary
Probability helps you understand random, unpredictable situations where multiple outcomes are possible., Es una medida de la probabilidad de un evento, y depende de la proporción de eventos y posibles resultados, si todos esos resultados son igualmente probables.