investigación correlacional: búsqueda de relaciones entre Variables
en contraste con la investigación descriptiva, que está diseñada principalmente para proporcionar imágenes estáticas, la investigación correlacional involucra la medición de dos o más variables relevantes y una evaluación de la relación entre o entre esas variables., Por ejemplo, las variables de altura y peso están sistemáticamente relacionadas (correlacionadas) porque las personas más altas generalmente pesan más que las personas más bajas. De la misma manera, el tiempo de estudio y los errores de memoria también están relacionados, porque cuanto más tiempo se le da a una persona para estudiar una lista de palabras, menos errores cometerá. Cuando hay dos variables en el diseño de la investigación, una de ellas se denomina variable predictora y la otra variable de resultado., El diseño de la investigación se puede visualizar así, donde la flecha curva representa la correlación esperada entre las dos variables:
figura 2.2.2

una forma de organizar los datos de un estudio correlacional con dos variables es graficar los valores de cada una de las variables medidas utilizando un gráfico de dispersión. Como puede ver en la figura 2.10 «ejemplos de gráficos de dispersión», un gráfico de dispersión es una imagen visual de la relación entre dos variables., Se traza un punto para cada individuo en la intersección de sus puntuaciones para las dos variables. Cuando la asociación entre las variables en el gráfico de dispersión se puede aproximar fácilmente con una línea recta, como en las partes (a) y (b) de la figura 2.10 «ejemplos de gráficos de dispersión», se dice que las variables tienen una relación lineal.
Cuando la línea recta indica que los individuos que tienen valores superiores a la media para una variable también tienden a tener valores superiores a la media para la otra variable, como en la Parte (a), se dice que la relación es lineal positiva., Entre los ejemplos de relaciones lineales positivas se incluyen las relaciones entre la altura y el peso, entre la educación y los ingresos, y entre la edad y las habilidades matemáticas en los niños. En cada caso, las personas que obtienen una puntuación más alta en una de las variables también tienden a obtener una puntuación más alta en la otra variable. Las relaciones lineales negativas, por el contrario, como se muestra en la Parte (b), ocurren cuando los valores por encima de la media para una variable tienden a asociarse con valores por debajo de la media para la otra variable., Ejemplos de relaciones lineales negativas incluyen aquellas entre la edad de un niño y el número de pañales que el niño usa, y entre la práctica y los errores cometidos en una tarea de aprendizaje. En estos casos, las personas que obtienen una puntuación más alta en una de las variables tienden a obtener una puntuación más baja en la otra variable.
Las relaciones entre variables que no se pueden describir con una línea recta se conocen como relaciones no lineales. La Parte (c) de la figura 2.10 «ejemplos de gráficos de dispersión» muestra un patrón común en el que la distribución de los puntos es esencialmente aleatoria., En este caso no hay ninguna relación en absoluto entre las dos variables, y se dice que son independientes. Las partes (d) y (e) de la figura 2.10 «ejemplos de diagramas de dispersión» muestran patrones de Asociación en los que, aunque hay una asociación, los puntos no están bien descritos por una sola línea recta. Por ejemplo, la Parte (d) muestra el tipo de relación que ocurre con frecuencia entre la ansiedad y el rendimiento., Los aumentos en la ansiedad de niveles bajos a moderados están asociados con aumentos en el rendimiento, mientras que los aumentos en la ansiedad de niveles moderados a altos están asociados con disminuciones en el rendimiento. Las relaciones que cambian de dirección y por lo tanto no se describen por una sola línea recta se denominan relaciones curvilíneas.
la Figura 2.10 Ejemplos de diagramas de Dispersión
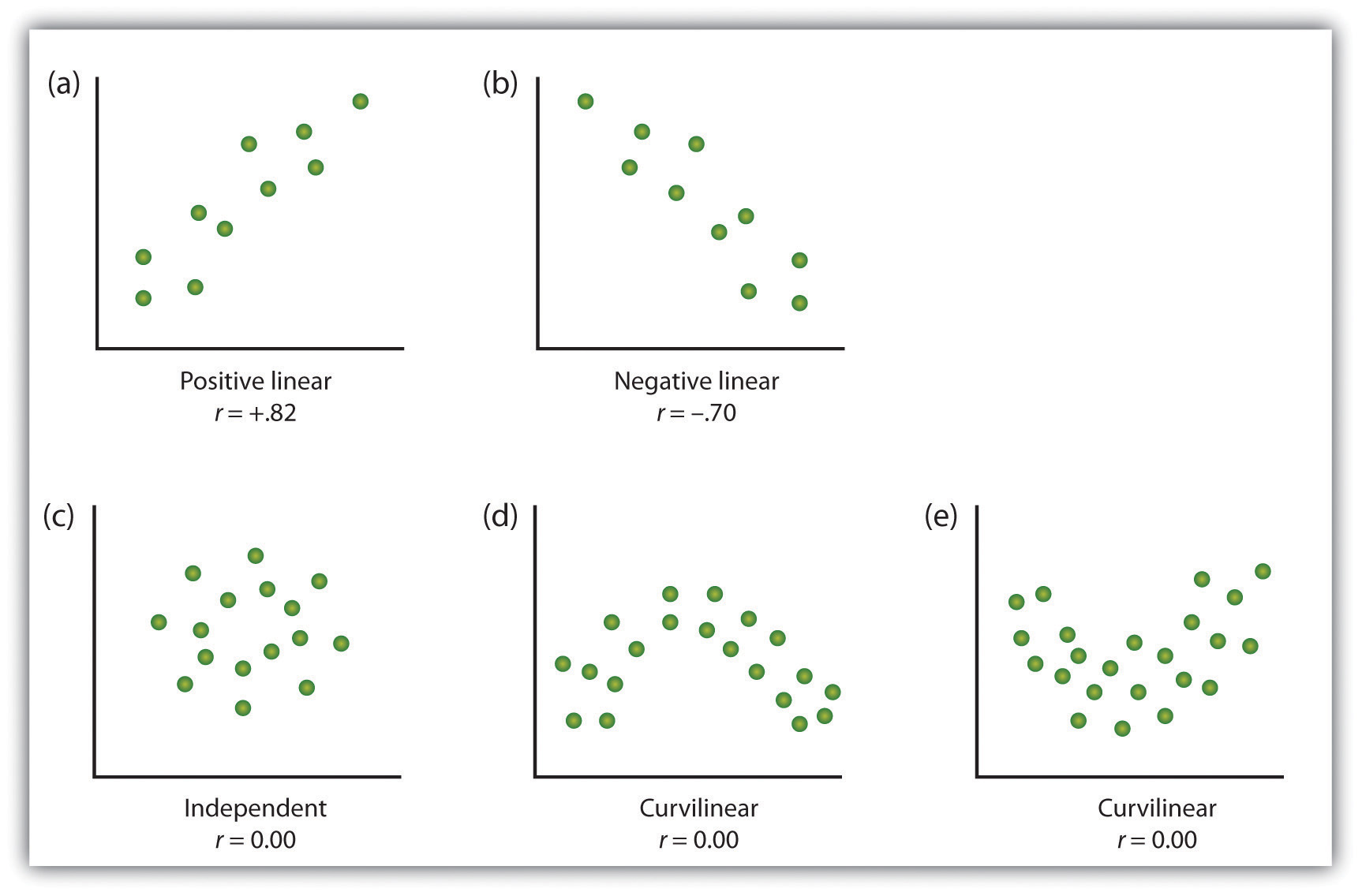
Algunos ejemplos de las relaciones entre dos variables, como se muestra en los diagramas de dispersión., Tenga en cuenta que el coeficiente de correlación de Pearson (r) entre las variables que tienen relaciones curvilíneas probablemente será cercano a cero.
adaptado de Stangor, C. (2011). Research methods for the behavioral sciences (4th ed.). Vista a la montaña, CA: Cengage.
la medida estadística más común de la fuerza de las relaciones lineales entre variables es el coeficiente de correlación de Pearson, que está simbolizado por la letra r. el valor del coeficiente de correlación varía de R = -1,00 A r = +1,00., La dirección de la relación lineal se indica por el signo del coeficiente de correlación. Valores positivos de r (como r=.54 o r = .67) indican que la relación es lineal positiva (es decir, el patrón de los puntos en el gráfico de dispersión se extiende desde la parte inferior izquierda a la parte superior derecha), mientras que los valores negativos de r (como r = –.30 o r= -.72) indican relaciones lineales negativas (es decir, los puntos van de la parte superior izquierda a la parte inferior derecha). La fuerza de la relación lineal está indexada por la distancia del coeficiente de correlación desde cero (su valor absoluto)., Por ejemplo, r = –.54 es una relación más fuerte que r=.30, y r=.72 es una relación más fuerte que r = –.57. Debido a que el coeficiente de correlación de Pearson solo mide relaciones lineales, las variables que tienen relaciones curvilíneas no están bien descritas por r, y la correlación observada será cercana a cero.
también es posible estudiar las relaciones entre más de dos medidas al mismo tiempo., Un diseño de investigación en el que se utiliza más de una variable predictora para predecir una sola variable de resultado se analiza a través de regresión múltiple (Aiken & West, 1991). La regresión múltiple es una técnica estadística, basada en coeficientes de correlación entre variables, que permite predecir una sola variable de resultado a partir de más de una variable predictora. Por ejemplo, la figura 2.11 «predicción del desempeño del trabajo a partir de tres Variables predictoras» muestra un análisis de regresión múltiple en el que se utilizan tres variables predictoras para predecir un único resultado., El uso del análisis de regresión múltiple muestra una ventaja importante de los diseños de investigación correlacional: se pueden usar para hacer predicciones sobre la puntuación probable de una persona en una variable de resultado (por ejemplo, desempeño laboral) basada en el conocimiento de otras variables.
figura 2.11 predicción del rendimiento del trabajo a partir de tres Variables predictoras
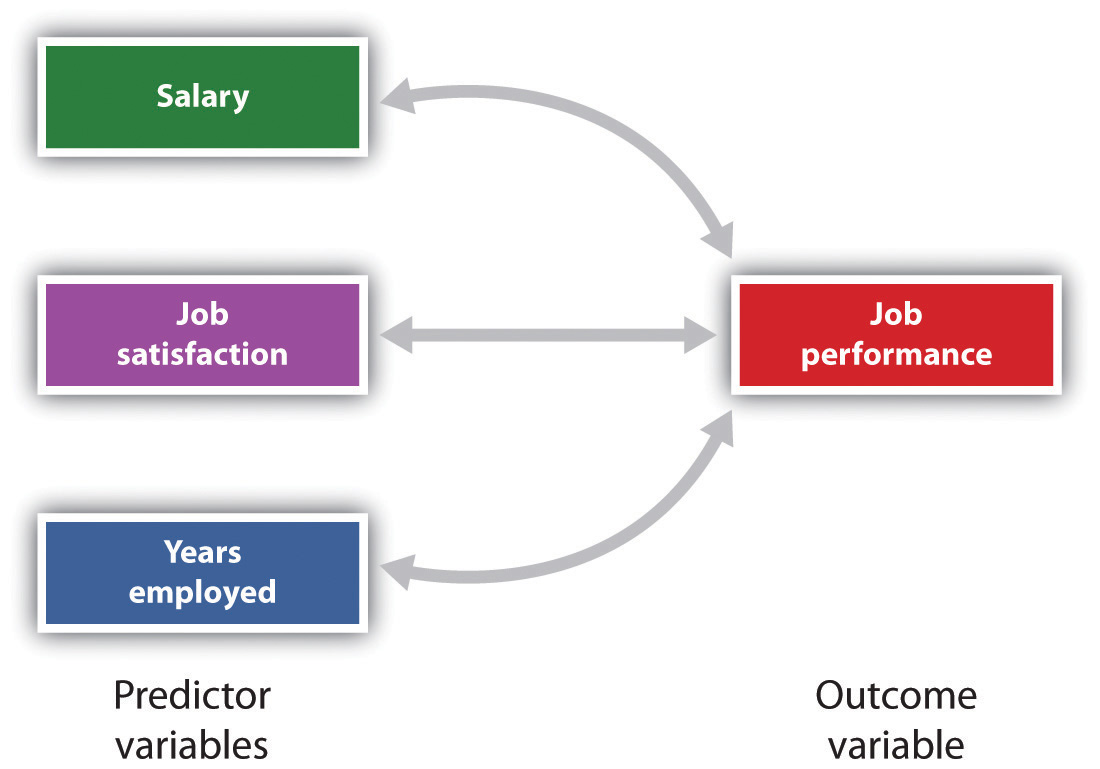
la regresión múltiple permite a los científicos predecir las puntuaciones en una sola variable de resultado utilizando más de un predictor variable.,
una limitación importante de los diseños de investigación correlacional es que no pueden ser utilizados para sacar conclusiones sobre las relaciones causales entre las variables medidas. Considere, por ejemplo, un investigador que ha hipotetizado que ver el comportamiento violento causará un aumento del juego agresivo en los niños. Ha recopilado, de una muestra de niños de CUARTO GRADO, una medida de cuántos programas de televisión violentos ve cada niño durante la semana, así como una medida de cuán agresivamente juega cada niño en el patio de recreo de la escuela., A partir de los datos recogidos, el investigador descubre una correlación positiva entre las dos variables medidas.
aunque esta correlación positiva parece apoyar la hipótesis del investigador, no puede ser tomada para indicar que ver televisión violenta causa comportamiento agresivo. Aunque el investigador se siente tentado a suponer que ver violentos de la televisión hace que el juego agresivo,
la Figura 2.2.2

hay otras posibilidades., Una posibilidad alternativa es que la dirección causal es exactamente opuesta a lo que se ha hipotetizado. Tal vez los niños que se han comportado agresivamente en la escuela desarrollan una emoción residual que los lleva a querer ver programas de televisión violentos en casa:
figura 2.2.2

aunque esta posibilidad puede parecer menos probable, no hay manera de descartar la posibilidad de tal causalidad inversa sobre la base de esta correlación observada., También es posible que tanto causal direcciones están funcionando y que las dos variables se causan unos a otros:
la Figura 2.2.2

otra posible explicación de la correlación observada es que ha sido producida por la presencia de una causal variable (también conocido como una tercera variable)., Una variable causal común es una variable que no forma parte de la hipótesis de investigación, pero que causa tanto el predictor como la variable de Resultado y, por lo tanto, produce la correlación observada entre ellos. En nuestro ejemplo, una posible variable común-causal es el estilo disciplinario de los padres de los niños. Los padres que usan un estilo de disciplina severo y punitivo pueden producir niños a los que les gusta ver televisión violenta y que se comportan agresivamente en comparación con niños cuyos padres usan una disciplina menos severa:
Figura 2.2.,2
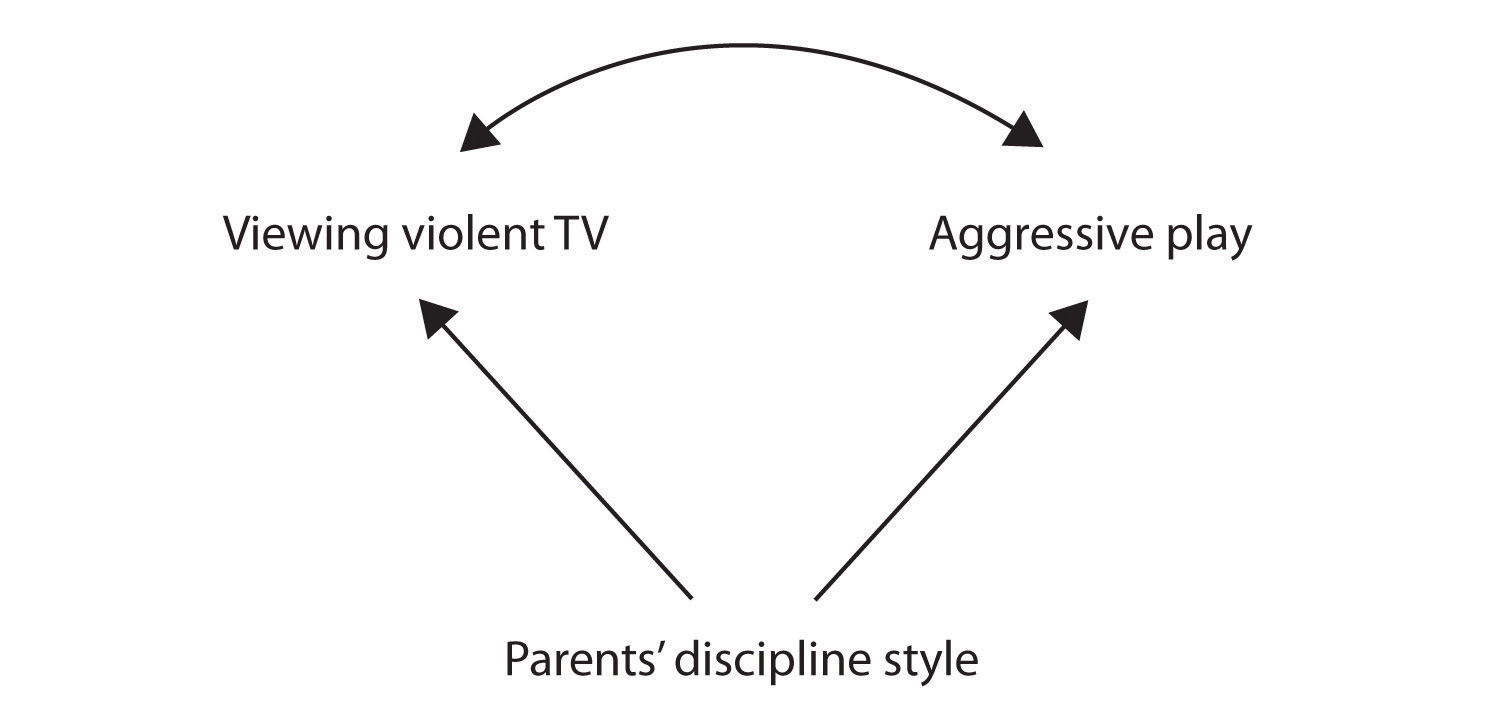
en este caso, la visualización de televisión y el juego agresivo estarían positivamente correlacionados (como lo indica la flecha curva entre ellos), aunque ninguno de los dos causó el otro, pero ambos fueron causados por el estilo disciplinario de los padres (las flechas rectas). Cuando las variables predictoras y de resultado son causadas por una variable causal común, se dice que la relación observada entre ellas es espuria., Una relación espuria es una relación entre dos variables en la que una variable causal común produce y «explica» la relación. Si los efectos de la variable causal común se eliminaran, o se controlaran, la relación entre el predictor y las variables de resultado desaparecería. En el ejemplo, la relación entre la agresión y la visualización de la televisión podría ser espuria porque al controlar el efecto del estilo disciplinario de los padres, la relación entre la visualización de la televisión y el comportamiento agresivo podría desaparecer.,
las variables causales comunes en los diseños de investigación correlacional pueden ser consideradas como variables «misteriosas» porque, al no haber sido medidas, su presencia e identidad son generalmente desconocidas para el investigador. Dado que no es posible medir todas las variables que podrían causar tanto las variables predictoras como las variables de resultado, la existencia de una variable común-causal desconocida es siempre una posibilidad. Por esta razón, nos queda la limitación básica de la investigación correlacional: la correlación no demuestra causalidad., Es importante que cuando lea sobre proyectos de investigación correlacional, tenga en cuenta la posibilidad de relaciones espurias y asegúrese de interpretar los hallazgos de manera apropiada. Aunque la investigación correlacional a veces se divulga como demostración de causalidad sin mencionar la posibilidad de causalidad inversa o variables causales comunes, los consumidores informados de la investigación, como usted, son conscientes de estos problemas interpretativos.
en suma, los diseños de investigación correlacional tienen fortalezas y limitaciones., Una fortaleza es que pueden ser utilizados cuando la investigación experimental no es posible porque las variables predictoras no pueden ser manipuladas. Los diseños correlacionales también tienen la ventaja de permitir al investigador estudiar el comportamiento tal como ocurre en la vida cotidiana. Y también podemos usar diseños correlacionales para hacer predicciones, por ejemplo, para predecir a partir de las puntuaciones de su batería de pruebas el éxito de los aprendices durante una sesión de capacitación. Sin embargo, no podemos utilizar esa información correlacional para determinar si la capacitación causó un mejor desempeño laboral. Para eso, los investigadores se basan en experimentos.,