Cifrado de Clave Pública

Criptografía de Clave Pública

a Diferencia de la criptografía de clave simétrica, no encontramos histórica uso de criptografía de clave pública. Es un concepto relativamente nuevo.

la criptografía simétrica era adecuada para organizaciones como gobiernos, militares y grandes corporaciones financieras que estaban involucradas en la comunicación clasificada.,

con la propagación de redes informáticas más inseguras en las últimas décadas, se sintió una verdadera necesidad de usar criptografía a mayor escala. Se encontró que la clave simétrica no era práctica debido a los desafíos que enfrentaba para la gestión de claves. Esto dio lugar a los criptosistemas de Clave Pública.

el proceso de cifrado y descifrado se muestra en la siguiente ilustración −

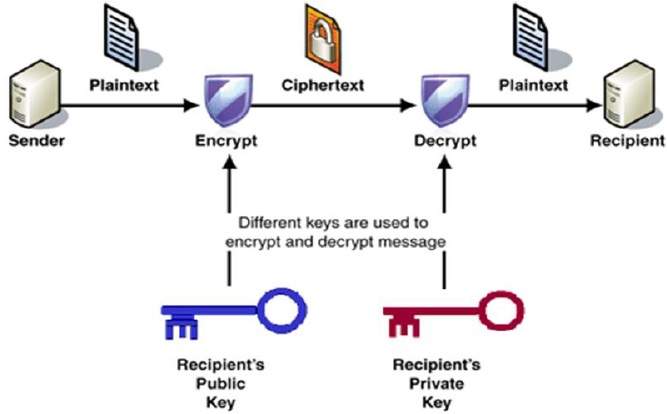
Las propiedades más importantes del esquema de cifrado de Clave Pública son −

• se utilizan diferentes claves para el cifrado y descifrado., Esta es una propiedad que establece este esquema diferente de symmetric encryption scheme.

• cada receptor posee una clave de descifrado única, generalmente conocida como su Clave Privada.

• El receptor necesita publicar una clave de cifrado, conocida como su Clave Pública.

• se necesita cierta seguridad de la autenticidad de una clave pública en este esquema para evitar la suplantación por parte del adversario como receptor. En general, este tipo de criptosistema involucra a un tercero de confianza que certifica que una clave pública en particular pertenece solo a una persona o entidad específica.,

• el algoritmo de cifrado es lo suficientemente complejo como para prohibir que el atacante deduzca el texto plano del texto cifrado y la clave de cifrado (pública).

• aunque las claves privadas y públicas están relacionadas matemáticamente, no es factible calcular la Clave Privada a partir de la Clave Pública. De hecho, la parte inteligente de cualquier criptosistema de Clave Pública está en el diseño de una relación entre dos claves.

hay tres tipos de esquemas de cifrado de Clave Pública., Los discutimos en las siguientes secciones:

criptosistema RSA

Este criptosistema es uno de los sistemas iniciales. Sigue siendo el criptosistema más empleado incluso hoy en día. El sistema fue inventado por tres eruditos Ron Rivest, Adi Shamir y Len Adleman y, por lo tanto, se denomina criptosistema RSA.

veremos dos aspectos del criptosistema RSA, en primer lugar, la generación de pares de claves y, en segundo lugar, los Algoritmos de cifrado y descifrado.,

generación de par de claves RSA

cada persona o parte que desee participar en la comunicación mediante cifrado necesita generar un par de claves, a saber, Clave Pública y Clave Privada. El proceso seguido en la generación de claves se describe a continuación:

• generar el módulo RSA (n)

  • seleccionar dos primos grandes, p y q.

  • calcular n=p*q. para un cifrado fuerte e irrompible, deje que n sea un número grande, normalmente un mínimo de 512 bits.,

• Encontrar la Derivada de Número (e)

  • Número de e debe ser mayor que 1 y menor que (p − 1)(q − 1).

  • no debe haber un factor común para e y (p − 1) (q-1) excepto para 1. En otras palabras dos números e y (p – 1)(q – 1) son coprime.

• formar la Clave Pública

  • El par de números (n, e) formar la clave pública RSA y se hace pública.,

  • curiosamente, aunque n es parte de la Clave Pública, la dificultad en factorizar un número primo grande asegura que el atacante no pueda encontrar en tiempo finito los dos primos (p & q) utilizados para obtener n. Esta es la fuerza de RSA.

• generar la Clave Privada

  • La Clave Privada d se calcula a partir de p, q y e. para n y e dados, hay un número único d.

  • El número d es el inverso del módulo e(p – 1) (q – 1)., Esto significa que d es el número menor que (p – 1)(q – 1) tal que cuando se multiplica por e, es igual a 1 modulo (p – 1)(q – 1).

  • esta relación se escribe matemáticamente de la siguiente manera:

ed = 1 mod (p − 1)(q − 1)

El algoritmo euclidiano extendido toma p, q y e como entrada y da d como salida.

ejemplo

a continuación se muestra un ejemplo de generación de par de claves RSA. (Para facilitar la comprensión, los primos p & q tomados aquí son valores pequeños. Prácticamente, estos valores son muy altos).,

• sean dos primos p = 7 y q = 13. Por lo tanto, módulo n = pq = 7 x 13 = 91.

• seleccione e = 5, que es una opción válida ya que no hay número que sea factor común de 5 y(p − 1) (q− 1) = 6 × 12 = 72, excepto por 1.

• el par de números (n, e) = (91, 5) forma la Clave Pública y se puede poner a disposición de cualquier persona que desee poder enviarnos mensajes cifrados.

• Input p = 7, q = 13 y e = 5 para el algoritmo euclidiano extendido. La salida será d = 29.,

• compruebe que la d calculada es correcta calculando –

de = 29 × 5 = 145 = 1 mod 72

• por lo tanto, la Clave Pública es (91, 5) y las claves privadas es (91, 29).

cifrado y descifrado

Una vez que se ha generado el par de claves, el proceso de cifrado y descifrado es relativamente sencillo y computacionalmente fácil.

curiosamente, RSA no opera directamente en cadenas de bits como en el caso del cifrado de clave simétrica. Opera en números modulo n. Por lo tanto, es necesario representar el texto plano como una serie de números menores que n.,

cifrado RSA

• supongamos que el remitente desea enviar un mensaje de texto a alguien cuya clave pública es (n, e).

• el remitente representa el texto plano como una serie de números menores que n.

• para cifrar el primer texto plano P, que es un módulo de número n. el proceso de cifrado es un paso matemático simple como −

C = Pe mod n

• En otras palabras, el texto cifrado C es igual a texto plano p multiplicado por sí mismo e veces y luego reducido módulo n. esto significa que c es también un número menor que n.,

• volviendo a nuestro ejemplo de generación de claves con texto plano P = 10, obtenemos texto cifrado C −

C = 105 mod 91

descifrado RSA

• el proceso de descifrado para RSA también es muy sencillo. Supongamos que el receptor del par de Clave Pública (n, e) ha recibido un texto cifrado C.

• El receptor eleva C a la potencia de su clave privada d. el módulo de resultado n será el texto plano P.,

Plaintext = Cd mod n

• volviendo de nuevo a nuestro ejemplo numérico, el texto cifrado C = 82 se descifraría al número 10 utilizando la Clave Privada 29 −

Plaintext = 8229 mod 91 = 10

análisis RSA

la seguridad de RSA depende de las fortalezas de dos funciones separadas. El criptosistema RSA es la fuerza criptosistema de Clave Pública más popular de los cuales se basa en la dificultad práctica de factorizar los números muy grandes.,

• Función de cifrado − se considera una función unidireccional de convertir texto plano en texto cifrado y solo se puede invertir con el conocimiento de la clave privada D.

• generación de claves-la dificultad de determinar una clave privada a partir de una clave pública RSA es equivalente a factorizar el módulo n. Un atacante no puede usar el conocimiento de una clave pública RSA para determinar una clave privada RSA a menos que pueda factorizar n. div id=»3db477d92a»> los valores q al módulo n son fáciles, pero no es posible invertirlos.,

si cualquiera de estas dos funciones se demuestra que no es unidireccional, entonces RSA se romperá. De hecho, si se desarrolla una técnica de factorización eficiente, RSA ya no será segura.

la fuerza del cifrado RSA disminuye drásticamente contra los ataques si el número p y q no son números primos grandes y/ o la Clave Pública elegida e es un número pequeño.

Elgamal Cryptosystem

junto con RSA, hay otros criptosistemas de Clave Pública propuestos. Muchos de ellos se basan en diferentes versiones del problema del logaritmo discreto.,

el criptosistema de ElGamal, llamado variante de curva elíptica, se basa en el problema del logaritmo discreto. Deriva la fuerza de la suposición de que los logaritmos discretos no se pueden encontrar en un marco de tiempo práctico para un número dado, mientras que la operación inversa de la potencia se puede calcular de manera eficiente.

pasemos por una versión sencilla de ElGamal que trabaja con números modulo P. en el caso de variantes de curvas elípticas, se basa en sistemas numéricos bastante diferentes. ,

generación del par de claves de ElGamal

cada usuario de ElGamal cryptosystem genera el par de claves de la siguiente manera:

• eligiendo un p primo grande. generalmente se elige un número primo de 1024 a 2048 bits de longitud.

• elegir un elemento generador g.

  • Este número debe estar entre 1 y p − 1, pero no puede ser ningún número.

  • es un generador del grupo multiplicativo de enteros módulo P. Esto significa que para cada entero m co-primo A p, Hay un entero k tal que gk = a mod n.,

    por ejemplo, 3 es generador del grupo 5 (Z5 = {1, 2, 3, 4}).

N	3n	3n mod 5
1	3	3
2	9	4
3	27	2
4	81	1

• la Elección de la clave privada. La Clave Privada x es cualquier número mayor que 1 y menor que p-1.

• calcular parte de la Clave Pública., El valor y se calcula a partir de los parámetros p, g y la Clave Privada x de la siguiente manera −

y = gx mod p

• obteniendo la Clave Pública. La Clave Pública de ElGamal consta de tres parámetros (p, g, y).

  por ejemplo, supongamos que p = 17 y que g = 6 (se puede confirmar que 6 es un generador del grupo Z17). La Clave Privada x puede ser cualquier número mayor que 1 y menor que 71, por lo que elegimos x = 5. El valor y se calcula de la siguiente manera:

y = 65 mod 17 = 7

• Por lo tanto, la clave privada es 62 y la Clave Pública es (17, 6, 7).,

cifrado y descifrado

la generación de un par de claves ElGamal es comparativamente más simple que el proceso equivalente para RSA. Pero el cifrado y el descifrado son un poco más complejos que RSA.

Cifrado ElGamal

Supongamos que el remitente desea enviar un texto a alguien cuya ElGamal clave pública es (p, g, y), entonces −

• Remitente representa el texto como una serie de números de módulo p.

• Para cifrar el primer texto plano P, que es representado como un número módulo p., El proceso de cifrado para obtener el texto cifrado C es el siguiente −

  • Generar aleatoriamente un número k;
  • calcular dos valores C1 y C2, donde –

C1 = gk mod pC2 = (P*yk) mod p

• enviar el texto cifrado C, que consiste en los dos valores separados (C1, C2), enviados juntos.,

• en referencia a nuestro ejemplo de generación de claves de ElGamal dado anteriormente, el texto plano P = 13 se cifra de la siguiente manera:

  • genere aleatoriamente un número, digamos k = 10
  • calcule los dos valores C1 y C2, donde −

C1 = 610 mod 17C2 = (13*710) mod 17 = 9

• envíe el texto cifrado C = (C1, C2) = (15, 9).,

descifrado ElGamal

• para descifrar el texto cifrado (C1, C2) utilizando la Clave Privada x, se toman los siguientes dos pasos:

  • calcular la inversa modular de (C1)x módulo p, que es (C1) −x , generalmente conocido como factor de descifrado.,

  • obtenga el texto plano utilizando la siguiente fórmula −

C2 × (C1)-x mod p = Plaintext

• en nuestro ejemplo, para descifrar el texto cifrado C = (C1, C2) = (15, 9) utilizando la Clave Privada x = 5, el factor de descifrado es

15-5 mod 17 = 9

• extract plaintext P = (9 × 9) mod 17 = 13.

Elgamal Analysis

en el sistema ElGamal, cada usuario tiene una clave privada x. y tiene tres componentes de Clave Pública: módulo prime p, generador g y público y = GX mod P., La fuerza del ElGamal se basa en la dificultad del problema del logaritmo discreto.

El tamaño de la clave segura es generalmente > 1024 bits. Hoy en día, incluso 2048 bits de clave larga se utilizan. En el frente de la velocidad de procesamiento, Elgamal es bastante lento, se utiliza principalmente para protocolos de autenticación de claves. Debido a una mayor eficiencia de procesamiento, las variantes de curva elíptica de ElGamal son cada vez más populares.,

criptografía de curva elíptica (ECC)

criptografía de curva elíptica (ECC) es un término utilizado para describir un conjunto de herramientas y protocolos criptográficos cuya seguridad se basa en versiones especiales del problema del logaritmo discreto. No utiliza numbers modulo p.

ECC se basa en conjuntos de números que están asociados con objetos matemáticos llamados curvas elípticas. Hay reglas para agregar y calcular múltiplos de estos números, al igual que las hay para los números módulo P.,

ECC incluye Variantes de muchos esquemas criptográficos que fueron diseñados inicialmente para números modulares, como el cifrado ElGamal y el algoritmo de firma Digital.

se cree que el problema del logaritmo discreto es mucho más difícil cuando se aplica a puntos en una curva elíptica. Esto provoca el cambio de números módulo p a puntos en una curva elíptica. También se puede obtener un nivel de seguridad equivalente con llaves más cortas si utilizamos variantes basadas en curvas elípticas.,

Las claves más cortas dan como resultado dos beneficios:

• facilidad de administración de claves
• computación eficiente

estos beneficios hacen que las variantes de esquema de cifrado basadas en curvas elípticas sean altamente atractivas para aplicaciones donde los recursos informáticos están limitados.

esquemas RSA y Elgamal – una comparación

comparemos brevemente los esquemas RSA y ElGamal en los diversos aspectos.

RSA	ElGamal
es más eficiente para el cifrado.	es más eficiente para el descifrado.,
es menos eficiente para el descifrado.	es más eficiente para el descifrado.
para un nivel de seguridad particular, se requieren claves largas en RSA.	para el mismo nivel de seguridad, se requieren claves muy cortas.
es ampliamente aceptado y utilizado.	es nuevo y no muy popular en el mercado.