para usar la calculadora de ángulo de referencia, simplemente ingrese cualquier ángulo en el cuadro de ángulo para encontrar su ángulo de referencia, que es el ángulo agudo que corresponde al ángulo ingresado. La calculadora aplica automáticamente las reglas que revisaremos a continuación.
¿qué es un ángulo de Referencia, de todos modos?
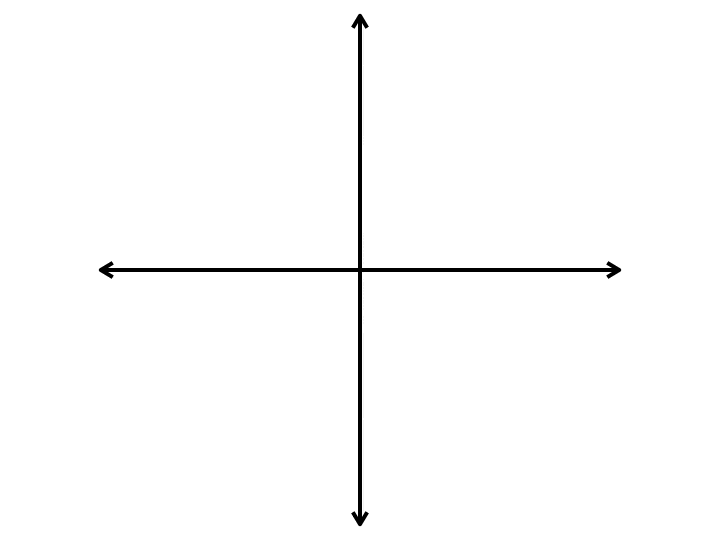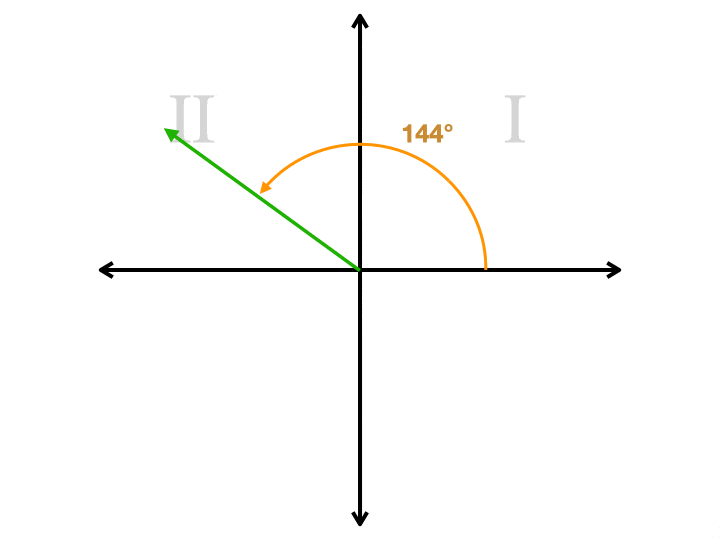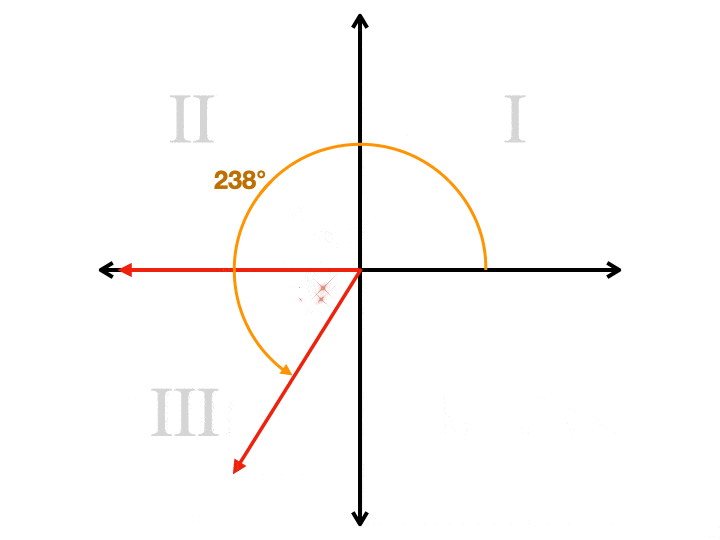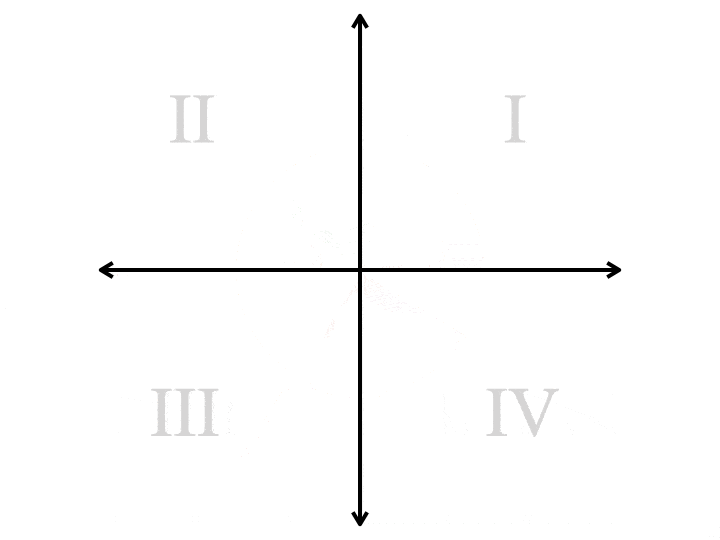
Imagine un plano de coordenadas. Digamos que queremos dibujar un ángulo de 144° en nuestro plano., Comenzamos en el lado derecho del eje x, donde las tres en punto están en un reloj. Giramos en sentido contrario a las agujas del reloj, que comienza moviéndose hacia arriba. Seguimos pasando el punto de 90° (la parte superior del eje y) hasta llegar a 144°. Dibujamos un rayo desde el origen, que es el centro del plano, hasta ese punto. Ahora tenemos un rayo que llamamos el lado terminal. Pero necesitamos dibujar un rayo más para hacer un ángulo. Tenemos una opción en este punto. Nuestro segundo rayo tiene que estar en el eje X. Si lo dibujamos desde el origen hacia el lado derecho, habremos dibujado un ángulo que mide 144°., Si lo dibujamos a la izquierda, habremos dibujado un ángulo que mide 36°. Este segundo ángulo es el ángulo de referencia. Siempre es el más pequeño de los dos ángulos, siempre será menor o igual a 90°, y siempre será positivo. Aquí hay una animación que muestra un ángulo de referencia para cuatro ángulos diferentes, cada uno de los cuales está en un cuadrante diferente. Observe cómo el segundo rayo está siempre en el eje X.
¿Cómo es el Ángulo de Referencia Útil?
el ángulo de referencia siempre tiene los mismos valores de función trigonométrica que el ángulo original. Observe los valores de la palabra allí., El signo puede no ser el mismo, pero el valor siempre lo será. Esto es útil para ángulos comunes como 45° y 60° que encontraremos una y otra vez. Una vez que conocemos sus valores de seno, coseno y tangente, también conocemos los valores para cualquier ángulo cuyo ángulo de referencia también es de 45° o 60°. En cuanto al signo, recuerde que el seno es positivo en el cuadrante 1 y 2 y el coseno es positivo en el cuadrante 1 y 4.
¿cómo encontramos el ángulo de referencia sin una calculadora?
Cómo encontramos el ángulo de referencia depende del cuadrante del lado terminal.,
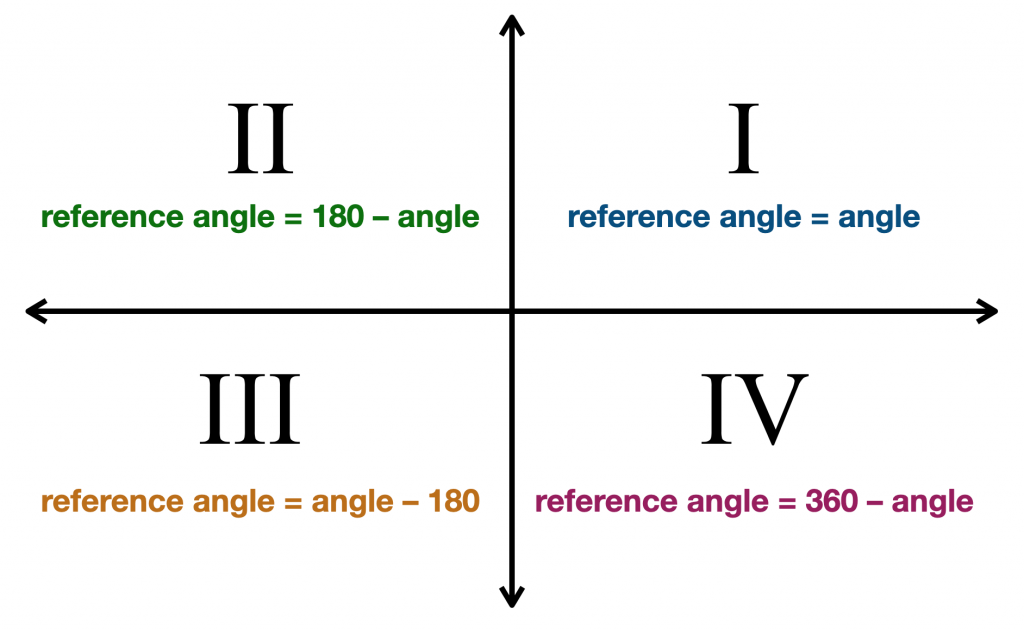
Cuando el lado terminal está en el primer cuadrante (ángulos de 0° a 90°), nuestro ángulo de referencia es el mismo que nuestro ángulo dado. Esto tiene sentido, ya que todos los ángulos en el primer cuadrante son inferiores a 90°. Por lo tanto, si nuestro ángulo dado es de 33°, entonces su ángulo de referencia también es de 33°.
Cuando el lado terminal está en el segundo cuadrante (ángulos de 90° a 180°), nuestro ángulo de referencia es de 180° menos nuestro ángulo dado. Por lo tanto, si nuestro ángulo dado es 110°, entonces su ángulo de referencia es 180° – 110° = 70°.,
Cuando el lado terminal está en el tercer cuadrante (ángulos de 180° a 270°), nuestro ángulo de referencia es nuestro ángulo dado menos 180°. Por lo tanto, si nuestro ángulo dado es 214°, entonces su ángulo de referencia es 214° – 180° = 34°.
Cuando el lado terminal está en el cuarto cuadrante (ángulos de 270° a 360°), nuestro ángulo de referencia es de 360° menos nuestro ángulo dado. Por lo tanto, si nuestro ángulo dado es 332°, entonces su ángulo de referencia es 360° – 332° = 28°.
¿qué pasa si nuestro ángulo es mayor que 360°?,
cuando un ángulo es mayor que 360°, eso significa que ha girado todo el camino alrededor del plano de coordenadas y siguió adelante. Para encontrar su ángulo de referencia, primero necesitamos encontrar su ángulo correspondiente entre 0° y 360°. Esto es fácil de hacer. Seguimos restando 360 hasta que esté por debajo de 360. Por ejemplo, si nuestro ángulo es de 544°, restaríamos 360° de él para obtener 184° (544° – 360° = 184°). Ahora notaríamos que está en el tercer cuadrante, así que restaríamos 180° de él para encontrar que nuestro ángulo de referencia es 4°.
¿qué pasa si nuestro ángulo es negativo?,
cuando un ángulo es negativo, movemos la otra dirección para encontrar nuestro lado terminal. Esto significa que nos movemos en el sentido de las agujas del reloj en lugar de en el sentido contrario al de las agujas del reloj al dibujarlo. O podemos calcularlo simplemente sumándolo a 360°. Por ejemplo, si nuestro ángulo dado es -110°, entonces lo agregaríamos a 360° para encontrar nuestro ángulo positivo de 250° (-110° + 360° = 250°). Ahora tendríamos que ver que estamos en el tercer cuadrante y aplicar esa regla para encontrar nuestro ángulo de referencia(250° – 180° = 70°).