Korrelationsforschung: Suche nach Beziehungen zwischen Variablen
Im Gegensatz zur deskriptiven Forschung, die hauptsächlich statische Bilder liefert, beinhaltet die Korrelationsforschung die Messung von zwei oder mehr relevanten Variablen und eine Bewertung der Beziehung zwischen oder zwischen diesen Variablen., Zum Beispiel sind die Größen-und Gewichtsvariablen systematisch verwandt (korreliert), da größere Menschen im Allgemeinen mehr wiegen als kürzere Menschen. In gleicher Weise hängen auch Studienzeit-und Gedächtnisfehler zusammen, denn je mehr Zeit eine Person zum Studium einer Liste von Wörtern hat, desto weniger Fehler macht sie. Wenn das Forschungsdesign zwei Variablen enthält, wird eine davon als Prädiktorvariable und die andere als Ergebnisvariable bezeichnet., Das Forschungsdesign kann folgendermaßen visualisiert werden, wobei der gekrümmte Pfeil die erwartete Korrelation zwischen den beiden Variablen darstellt:
Abbildung 2.2.2

Eine Möglichkeit, die Daten aus einer Korrelationsstudie mit zwei Variablen zu organisieren:
iv variablen ist die Darstellung der Werte jeder der gemessenen Variablen unter Verwendung eines Streudiagramms. Wie Sie in Abbildung 2.10 „Beispiele für Streudiagramme“ sehen können, ist ein Streudiagramm ein visuelles Bild der Beziehung zwischen zwei Variablen., Ein Punkt wird für jeden Einzelnen am Schnittpunkt seiner Punktzahlen für die beiden Variablen aufgetragen. Wenn die Assoziation zwischen den Variablen auf dem Streudiagramm leicht mit einer geraden Linie angenähert werden kann, wie in den Teilen (a) und (b) von Abbildung 2.10 „Beispiele für Streudiagramme“, sollen die Variablen eine lineare Beziehung haben.
Wenn die gerade Linie angibt, dass Personen, die überdurchschnittliche Werte für eine Variable haben, auch überdurchschnittliche Werte für die andere Variable haben, wie in Teil (a), wird die Beziehung als positiv linear bezeichnet., Beispiele für positive lineare Beziehungen sind die zwischen Größe und Gewicht, zwischen Bildung und Einkommen sowie zwischen Alter und mathematischen Fähigkeiten bei Kindern. In jedem Fall tendieren Personen, die bei einer der Variablen eine höhere Punktzahl erzielen, auch dazu, bei der anderen Variablen eine höhere Punktzahl zu erzielen. Negative lineare Beziehungen treten dagegen, wie in Teil (b) gezeigt, auf, wenn überdurchschnittliche Werte für eine Variable tendenziell mit unterdurchschnittlichen Werten für die andere Variable assoziiert werden., Beispiele für negative lineare Beziehungen sind solche zwischen dem Alter eines Kindes und der Anzahl der Windeln, die das Kind verwendet, sowie zwischen Üben und Fehlern bei einer Lernaufgabe. In diesen Fällen neigen Personen, die bei einer der Variablen eine höhere Punktzahl erzielen, dazu, bei der anderen Variablen eine niedrigere Punktzahl zu erzielen.
Beziehungen zwischen Variablen, die nicht mit einer geraden Linie beschrieben werden können, werden als nichtlineare Beziehungen bezeichnet. Teil (c) der Abbildung 2.10 „Beispiele für Streudiagramme“ zeigt ein gemeinsames Muster, bei dem die Verteilung der Punkte im Wesentlichen zufällig ist., In diesem Fall gibt es keine Beziehung zwischen den beiden Variablen, und Sie werden gesagt, um unabhängig zu sein. Teile (d) und (e) von Abbildung 2.10 „Beispiele für Streudiagramme“ zeigen Assoziationsmuster, bei denen die Punkte, obwohl es eine Assoziation gibt, nicht gut durch eine einzige gerade Linie beschrieben sind. Zum Beispiel zeigt Teil (d) die Art der Beziehung, die häufig zwischen Angst und Leistung auftritt., Erhöhungen der Angst von niedrigem bis mäßigem Niveau sind mit Leistungssteigerungen verbunden, während Erhöhungen der Angst von moderatem bis hohem Niveau mit Leistungseinbußen verbunden sind. Beziehungen, die sich in Richtung ändern und somit nicht durch eine einzige gerade Linie beschrieben werden, werden krummlinige Beziehungen genannt.
Abbildung 2.10 Beispiele für Streudiagramme
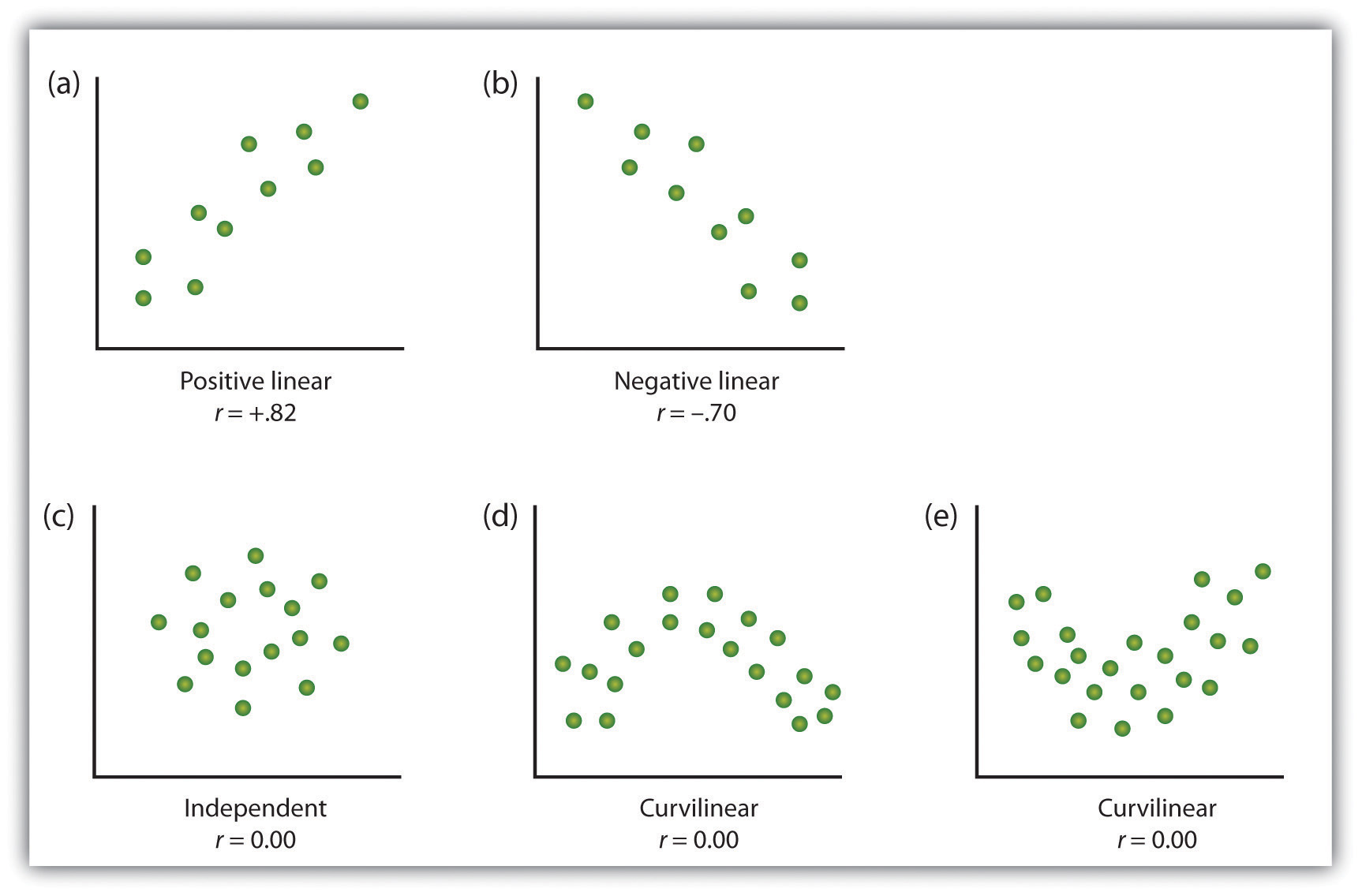
Einige Beispiele für Beziehungen zwischen zwei Variablen, wie in Streudiagrammen gezeigt., Beachten Sie, dass der Pearson-Korrelationskoeffizient (r) zwischen Variablen mit krummlinigen Beziehungen wahrscheinlich nahe Null liegt.
Adaptiert von Stangor, C. (2011). Forschungsmethoden für die Verhaltenswissenschaften (4.Aufl.). Mountain View, CA: Cengage.
Das häufigste statistische Maß für die Stärke linearer Beziehungen zwischen Variablen ist der Pearson-Korrelationskoeffizient, der durch den Buchstaben r symbolisiert wird. , Die Richtung der linearen Beziehung wird durch das Vorzeichen des Korrelationskoeffizienten angezeigt. Positive Werte von r (wie r = .54 oder r = .67) zeigen an, dass die Beziehung positiv linear ist (dh das Muster der Punkte auf dem Streudiagramm verläuft von unten links nach oben rechts), während negative Werte von r (wie r = –.30 oder r = –.72) zeigen negative lineare Beziehungen an (d. H. Die Punkte verlaufen von oben links nach unten rechts). Die Stärke der linearen Beziehung wird durch den Abstand des Korrelationskoeffizienten von Null (seinem absoluten Wert) indiziert., Zum Beispiel, r = –.54 ist eine stärkere Beziehung als r = .30 und r = .72 ist eine stärkere Beziehung als r = –.57. Da der Pearson-Korrelationskoeffizient nur lineare Beziehungen misst, werden Variablen mit krummlinigen Beziehungen nicht gut durch r beschrieben, und die beobachtete Korrelation liegt nahe Null.
Es ist auch möglich, Beziehungen zwischen mehr als zwei Maßnahmen gleichzeitig zu untersuchen., Ein Forschungsdesign, bei dem mehr als eine Prädiktorvariable zur Vorhersage einer einzelnen Ergebnisvariablen verwendet wird, wird durch multiple Regression analysiert (Aiken & West, 1991). Multiple Regression ist eine statistische Technik, die auf Korrelationskoeffizienten zwischen Variablen basiert und es ermöglicht, eine einzelne Ergebnisvariable aus mehr als einer Prädiktorvariablen vorherzusagen. Abbildung 2.11 „Vorhersage der Arbeitsleistung aus drei Prädiktorvariablen“ zeigt beispielsweise eine Multiple Regressionsanalyse, bei der drei Prädiktorvariablen verwendet werden, um ein einzelnes Ergebnis vorherzusagen., Die Verwendung der multiplen Regressionsanalyse zeigt einen wichtigen Vorteil von Korrelationsforschungsdesigns—sie können verwendet werden, um Vorhersagen über die wahrscheinliche Punktzahl einer Person für eine Ergebnisvariable (z. B. Arbeitsleistung) basierend auf Kenntnissen anderer Variablen zu treffen.
Abbildung 2.11 Vorhersage der Auftragsleistung aus drei Prädiktorvariablen
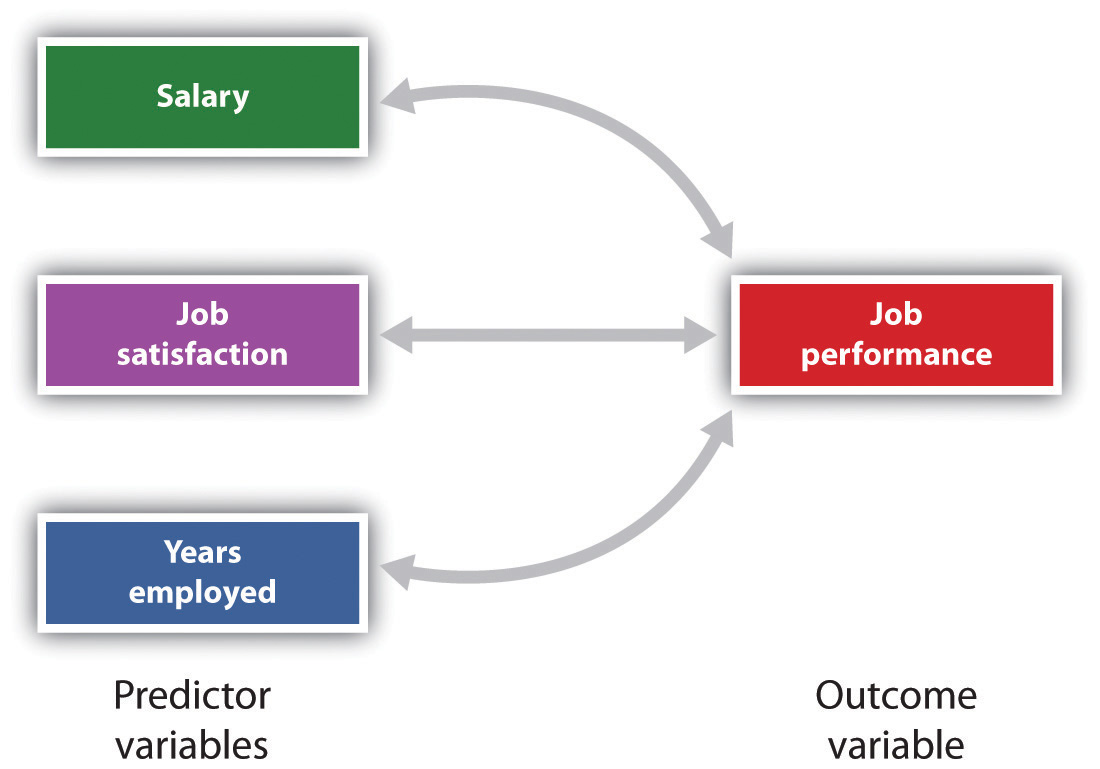
Mit der multiplen Regression können Wissenschaftler die Ergebnisse einer einzelnen Ergebnisvariablen mithilfe von mehr als einer Prädiktorvariablen vorhersagen.,
Eine wichtige Einschränkung von Korrelationsforschungsdesigns besteht darin, dass sie nicht verwendet werden können, um Rückschlüsse auf die kausalen Beziehungen zwischen den gemessenen Variablen zu ziehen. Betrachten Sie zum Beispiel einen Forscher, der die Hypothese aufgestellt hat, dass das Betrachten von gewalttätigem Verhalten bei Kindern zu erhöhtem aggressivem Spiel führt. Er hat aus einer Stichprobe von Kindern der vierten Klasse ein Maß dafür gesammelt, wie viele gewalttätige Fernsehsendungen jedes Kind während der Woche sieht, sowie ein Maß dafür, wie aggressiv jedes Kind auf dem Schulspielplatz spielt., Aus seinen gesammelten Daten entdeckt der Forscher eine positive Korrelation zwischen den beiden gemessenen Variablen.
Obwohl diese positive Korrelation die Hypothese des Forschers zu stützen scheint, kann nicht darauf hingewiesen werden, dass das Betrachten von gewalttätigem Fernsehen aggressives Verhalten verursacht. Obwohl der Forscher versucht ist anzunehmen, dass das Betrachten von gewalttätigem Fernsehen aggressives Spiel verursacht,
Abbildung 2.2.2

Es gibt andere Möglichkeiten., Eine alternative Möglichkeit besteht darin, dass die kausale Richtung genau entgegengesetzt zu dem ist, was angenommen wurde. Vielleicht entwickeln Kinder, die sich in der Schule aggressiv verhalten haben, eine restliche Aufregung, die dazu führt, dass sie zu Hause gewalttätige Fernsehsendungen sehen möchten:
Abbildung 2.2.2

Obwohl diese Möglichkeit weniger wahrscheinlich erscheint, es gibt keine Möglichkeit, die Möglichkeit einer solchen umgekehrten Kausalität aufgrund dieser beobachteten Korrelation auszuschließen., Es ist auch möglich, dass beide Kausalrichtungen funktionieren und dass sich die beiden Variablen gegenseitig verursachen:
Abbildung 2.2.2

Eine weitere mögliche Erklärung für die beobachtete Korrelation ist, dass sie von der vorhandensein einer gemeinsamen kausalen Variablen (auch als dritte Variable bezeichnet)., Eine Common-Causal-Variable ist eine Variable, die nicht Teil der Forschungshypothese ist, aber sowohl den Prädiktor als auch die Ergebnisvariable verursacht und somit die beobachtete Korrelation zwischen ihnen erzeugt. In unserem Beispiel ist eine mögliche häufig-kausale Variable der Disziplinstil der Eltern der Kinder. Eltern, die einen harten und strafenden Disziplinstil anwenden, können Kinder hervorbringen, die beide gerne gewalttätig fernsehen und sich im Vergleich zu Kindern, deren Eltern weniger harte Disziplin anwenden, aggressiv verhalten:
Abbildung 2.2.,2
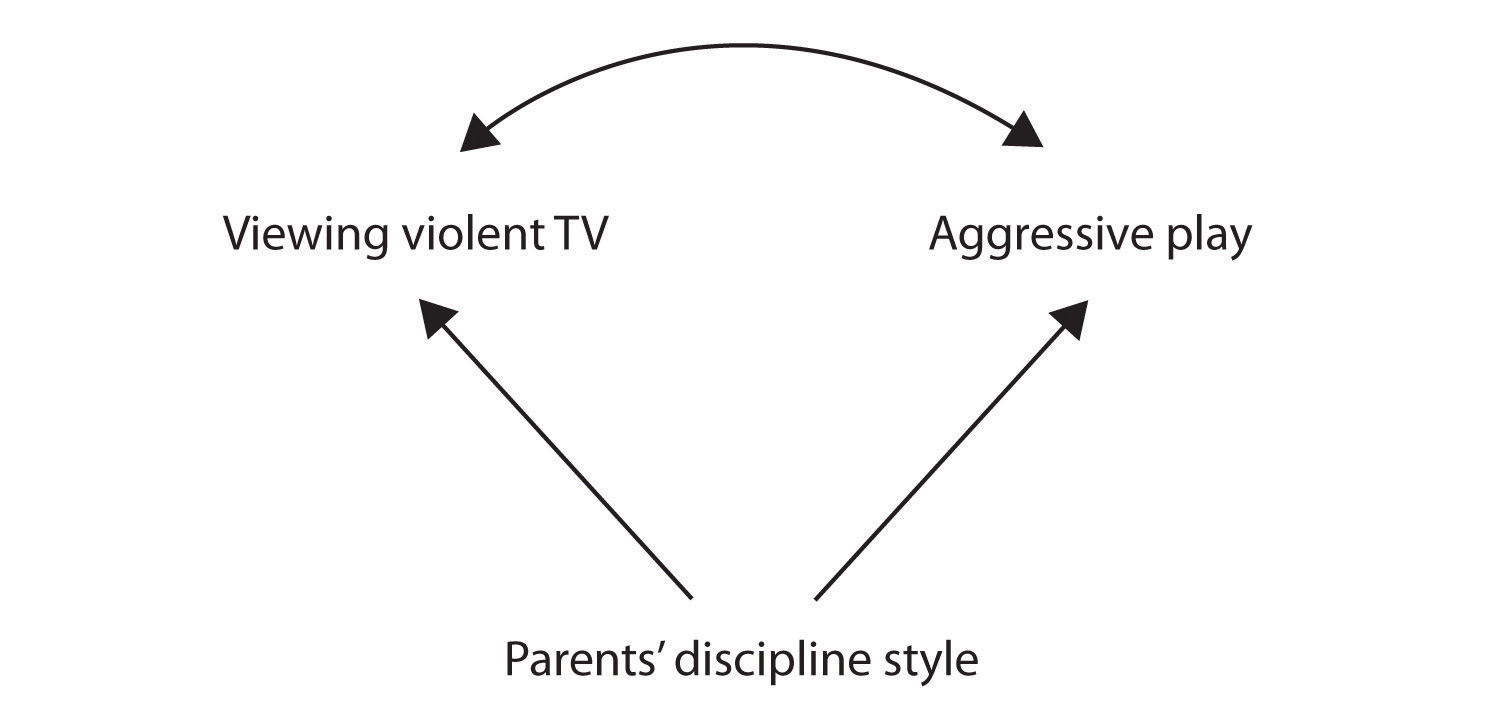
In diesem Fall wären Fernsehen und aggressives Spiel positiv korreliert (wie durch den gekrümmten Pfeil zwischen ihnen angezeigt), obwohl keiner der beiden den anderen verursachte, aber beide durch den Disziplinstil der Eltern (die geraden Pfeile) verursacht wurden. Wenn die Prädiktor-und Ergebnisvariablen beide durch eine gemeinsame kausale Variable verursacht werden, wird die beobachtete Beziehung zwischen ihnen als falsch bezeichnet., Eine falsche Beziehung ist eine Beziehung zwischen zwei Variablen, in der eine gemeinsam-kausale Variable die Beziehung erzeugt und „erklärt“. Wenn Effekte der Common-Causal-Variablen weggenommen oder kontrolliert würden, würde die Beziehung zwischen dem Prädiktor und den Ergebnisvariablen verschwinden. In dem Beispiel könnte die Beziehung zwischen Aggression und Fernsehbetrachtung falsch sein, da durch die Kontrolle der Wirkung des Disziplinierungsstils der Eltern die Beziehung zwischen Fernsehbetrachtung und aggressivem Verhalten verschwinden könnte.,
Common-kausalen Variablen in der correlational Forschung designs gedacht werden kann, wie „mystery“ – Variablen, weil Sie nicht gemessen worden ist, ist Ihre Anwesenheit und Identität sind in der Regel unbekannt, die Forscher. Da es nicht möglich ist, jede Variable zu messen, die sowohl die Prädiktor-als auch die Ergebnisvariablen verursachen könnte, ist die Existenz einer unbekannten Common-Causal-Variablen immer eine Möglichkeit. Aus diesem Grund bleibt uns die grundlegende Einschränkung der Korrelationsforschung: Korrelation zeigt keine Kausalität., Es ist wichtig, dass Sie beim Lesen von Korrelationsforschungsprojekten die Möglichkeit falscher Beziehungen berücksichtigen und die Ergebnisse angemessen interpretieren. Obwohl Korrelationsforschung manchmal als Kausalität demonstriert wird, ohne die Möglichkeit einer umgekehrten Kausalität oder häufig-kausalen Variablen zu erwähnen, sind sich informierte Forschungskonsumenten wie Sie dieser Interpretationsprobleme bewusst.
In der Summe correlational Forschung designs haben beide stärken und Schwächen., Eine Stärke ist, dass sie verwendet werden können, wenn experimentelle Forschung nicht möglich ist, da die Prädiktorvariablen nicht manipuliert werden können. Korrelationsdesigns haben auch den Vorteil, dass der Forscher das Verhalten im Alltag untersuchen kann. Und wir können auch Korrelationsentwürfe verwenden, um Vorhersagen zu treffen—zum Beispiel, um aus den Ergebnissen ihrer Testreihe den Erfolg von Job-Auszubildenden während einer Trainingseinheit vorherzusagen. Wir können solche Korrelationsinformationen jedoch nicht verwenden, um festzustellen, ob das Training zu einer besseren Arbeitsleistung geführt hat. Dafür verlassen sich Forscher auf Experimente.,