Sandsynlighed
Læring Mål(s)
· Definere tilfælde, resultatet, retssag, enkel begivenhed, prøve plads og beregne sandsynligheden for, at en begivenhed vil finde sted.
· Beregn sandsynligheden for begivenheder for mere komplekse resultater.
· Løs applikationer, der involverer sandsynligheder.
introduktion
Sandsynlighed giver et mål for, hvor sandsynligt det er, at der vil opstå noget., Det er et tal mellem og inklusive numrene 0 og 1. Det kan skrives som en brøkdel, en decimal eller en procent.

plukning af tal betyder tilfældigt, at der ikke er nogen bestemt rækkefølge, de vælges i. Mange spil bruger terninger eller spinnere til at generere tal tilfældigt. Hvis du forstår, hvordan du beregner sandsynligheder, kan du tage tankevækkende beslutninger om, hvordan du spiller disse spil ved at kende sandsynligheden for forskellige resultater.,
definitioner
først skal du kende nogle udtryk relateret til Sandsynlighed. Når man arbejder med Sandsynlighed, kaldes en tilfældig handling eller række handlinger en prøve. Et resultat er resultatet af et forsøg, og en begivenhed er en særlig samling af resultater. Begivenheder beskrives normalt ved hjælp af en fælles karakteristik af resultaterne.
lad os anvende dette sprog for at se, hvordan udtrykkene fungerer i praksis. Nogle spil kræver rullende en matrice med seks sider, nummereret fra 1 til 6. (Dice er flertallet af die.,) Diagrammet nedenfor illustrerer brugen af forsøg, resultat og begivenhed til et sådant spil:
Bemærk, at en samling af resultater sættes i seler og adskilles af kommaer.
en simpel begivenhed er en begivenhed med kun et resultat. Rolling a 1 ville være en simpel begivenhed, fordi der kun er et resultat, der virker-1! At rulle mere end en 5 ville også være en simpel begivenhed, fordi begivenheden kun inkluderer 6 som et gyldigt resultat. En sammensat begivenhed er en begivenhed med mere end et resultat. For eksempel, i rullende en seks-sidet dør, rullende et jævnt tal kunne forekomme med en af tre resultater: 2, 4, og 6.,
Når du ruller en seks-sidet dø mange gange, bør du ikke forvente, at noget resultat vil ske oftere end et andet (forudsat at det er en retfærdig dø). Resultaterne i en situation som denne siges at være lige så sandsynlige. Det er meget vigtigt at genkende, når resultaterne er lige så sandsynlige, når man beregner Sandsynlighed. Da hvert resultat i die-rolling-forsøget er lige så sandsynligt, ville du forvente at få hvert resultat ![]() af rullerne., Det er, hvad du ville forvente
af rullerne., Det er, hvad du ville forvente ![]() af ruller til at være 1,
af ruller til at være 1, ![]() af ruller til at være 2
af ruller til at være 2 ![]() af ruller til at være 3, og så videre.
af ruller til at være 3, og så videre.
en spinner er opdelt i fire lige store dele, hver farvet med en anden farve som vist nedenfor. Når denne spinner er spundet, peger pilen på en af farverne. Er resultaterne lige sandsynlige?
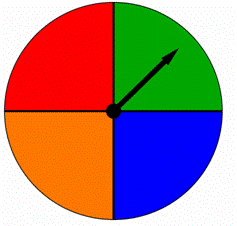
a) ja, de er lige så sandsynlige.
B) Nej, De er ikke lige sandsynlige.,
Sandsynligheden for Begivenheder
sandsynligheden af en hændelse er, hvor ofte det kan forventes at forekomme. Det er forholdet mellem størrelsen af begivenheden plads til størrelsen af prøven plads.
først skal du bestemme størrelsen på prøvepladsen. Størrelsen af prøvepladsen er det samlede antal mulige resultater. For eksempel, når du ruller 1 dør, prøven plads er 1, 2, 3, 4, 5, is or 6. Så størrelsen af prøvepladsen er 6.
derefter skal du bestemme størrelsen på begivenhedsrummet., Begivenhedsområdet er antallet af resultater i tilfælde af at du er interesseret i. Arrangementet plads til at rulle et tal mindre end tre er 1 eller 2. Så størrelsen af begivenheden plads er 2.
for lige sandsynlige resultater kan sandsynligheden for en begivenhed E skrives P(E).
![]()
|
Eksempel |
||
|
Problem |
Et spil kræver, at der kastes en seks-sidet terning nummereret fra 1 til 6., Hvad er sandsynligheden for at rulle et lige antal? |
|
|
Prøve plads = {1, 2, 3, 4, 5, 6}
Event plads = {2, 4, 6} |
Først skal du finde den prøve, rum og begivenhed plads. Prøven plads er alle de mulige udfald, og begivenheden plads er resultaterne i begivenheden. I dette tilfælde er begivenheden “rullende et lige antal.,” |
|
|
|
Da det udfald er lige sandsynlige, er sandsynligheden for, at begivenheden er forholdet mellem begivenhed plads til at prøve plads., |
|
|
Svar |
P(lige tal) = |
|
Det er en almindelig praksis med sandsynligheder, som med brøker i almindelighed, til at forenkle en sandsynlighed i laveste tal siden, der gør det lettere for de fleste mennesker at få en fornemmelse af hvor stor den er. Medmindre der er grund til ikke at gøre det, udtrykke alle endelige sandsynligheder i Laveste Vilkår.,
en spinner er opdelt i lige store dele, hver farvet med en anden farve som vist nedenfor., Find sandsynligheden for at dreje blå eller grøn på dette spinner:
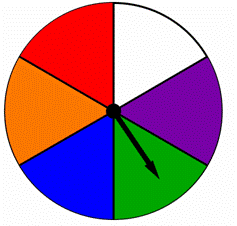
A) ![]()
B) ![]()
C) 2
D) 6
Optælling Metoder til at finde Prøve Rum
De mest vanskelige ting for at beregne en sandsynlighed kan være at finde størrelsen af stikprøven plads, især hvis der er to eller flere forsøg. Der er flere tællemetoder, der kan hjælpe.,
den første til at se på er at lave et diagram. I eksemplet nedenfor, Tori er spejlvende to mønter. Så du skal bestemme prøvepladsen omhyggeligt. Et diagram som det, der er vist i det følgende eksempel, er en god tilgang.
|
Eksempel |
||||
|
Problem |
Tori er spejlvende et par mønter, og bemærke hvor mange flips af “hoveder”, hun får. Hvad er sandsynligheden for, at hun vender 2 hoveder?, Hvad er sandsynligheden for, at hun kun vender 1 hoved?,15ecf6″>T |
T |
TT |
|
sample space: {HH, HT, TH, TT}
event space for 2 heads: {HH}
event space for 1 head: {HT, TH}
Create a chart to record the results of flipping the first coin, followed by the result of flipping the second coin.,
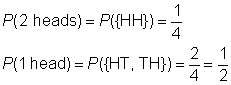
Da det udfald er lige sandsynlige, er sandsynligheden for, at begivenheden er forholdet mellem begivenhed plads til at prøve plads.,
Svar
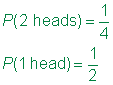
I eksemplet nedenfor, prøve plads til Tori er enkel, da kun én dør, er ved at blive rullet. Imidlertid, da James ruller to dør, et diagram hjælper med at organisere Informationen.,
|
Eksempel |
||||||||
|
Problem |
Tori væltede en seks-sidet terning, og ønskede at få et resultat, af enten 1 eller 4. James rullede to seks-sidet terninger, en blå og en rød, og ønskede at få et resultat af både en 1 og en 3, på samme tid. Hvilken begivenhed har større sandsynlighed?, |
|||||||
|
Tori’s sample space: {1, 2, 3, 4, 5, 6}
Tori’s event space: {1, 4}
Tori:
|
First, find the sample space and the event space for the two trials., For Toris retssag er dette ligetil. da resultaterne er lige sandsynlige, er sandsynligheden for begivenheden forholdet mellem begivenhedsrum og prøveplads.,316594724″> 6 |
6,1 |
6,2 |
6,3 |
6,4 |
6,5 |
6,6 |
|
James’ sample space has 36 outcomes.,
James’ begivenhedsrum har 2 resultater.
det er ikke så indlysende for James’ retssag, da han ruller to terninger. Brug et diagram til at finde mulighederne.
der er 36 resultater. Af disse er der 2, der har både 1 og 3.,
James: ![]()
Da det udfald er lige sandsynlige, er sandsynligheden for, at begivenheden er forholdet mellem begivenhed plads til at prøve plads.
Svar
Tori ‘ s tilfælde har en større sandsynlighed.,
Du kan også bruge et træ diagram til at bestemme prøve plads. Et træ diagram har en gren for alle mulige udfald for hver begivenhed.
Antag, at et skab, har tre par bukser (sort, hvid og grøn), fire shirts (grøn, hvid, lilla og gul), og to par sko (sort og hvid). Hvor mange forskellige tøj kan der laves? Der er 3 valg til bukser, 4 valg til skjorter og 2 valg til sko., Til vores trædiagram, lad os bruge B til sort, W for hvid, G for grøn, P for lilla og Y for gul.
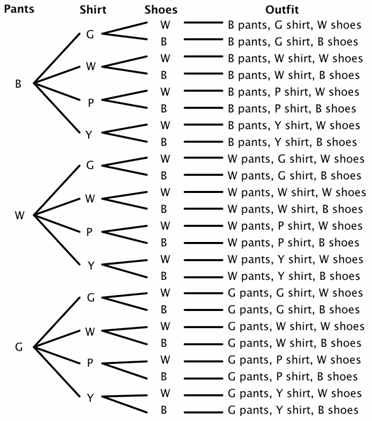
Du kan se fra trædiagrammet, at der er 24 mulige tøj (nogle måske ikke gode valg) i prøvepladsen.
nu Kan du ret nemt løse nogle sandsynlighedsproblemer. For eksempel, Hvad er sandsynligheden for, at hvis du lukker øjnene og vælger tilfældigt, ville du vælge bukser og sko med samme farve? Du kan se, at der er 8 tøj, hvor bukserne og skoene matcher.,
![]()
Som du har set, når en retssag omfatter mere end et tilfældigt element, såsom at bladre mere end en mønt eller rullende mere end én dør, behøver du ikke altid nødt til at identificere hver resultat i prøven plads til at beregne en sandsynlighed. Du behøver kun antallet af resultater.
det grundlæggende Tælleprincip er en måde at finde antallet af resultater uden at liste og tælle hver eneste af dem.,
det grundlæggende Tælleprincip
Hvis en begivenhed har p mulige resultater, og en anden begivenhed har m mulige resultater, er der i alt p • m mulige resultater for de to begivenheder.
eksempler
· rullende to seks-sidede terninger: hver terning har 6 lige sandsynlige resultater, så prøvepladsen er 6 • 6 eller 36 lige så sandsynlige resultater.
· Flipping tre mønter: hver mønt har 2 lige så sandsynlige resultater, så prøvepladsen er 2 • 2 • 2 eller 8 lige så sandsynlige resultater.,
· rullende en seks-sidet Matrice og spejlvende en mønt: prøvepladsen er 6 • 2 eller 12 lige så sandsynlige resultater.
så du kunne bruge det grundlæggende Tællingsprincip til at finde ud af, hvor mange tøj der er i det foregående eksempel. Der er 3 valg til bukser, 4 valg til skjorter og 2 valg til sko. Ved hjælp af det grundlæggende Tælleprincip har du 4 • 3 • 2 = 24 forskellige outfits.,
|
Eksempel |
||
|
Problem |
Barry frivillige på en velgørende gåtur til at lave frokost til alle de andre frivillige. I hver pose, han sætter: · en af to sandwich (jordnøddesmør og gelé eller kalkun og ost), · en af tre chips (almindelig kartoffel chips, bagt kartoffel, chips eller majs chips), · et stykke frugt (et æble eller en appelsin)., han glemte at markere, hvad der var i poserne. Antages det, at hvert valg er lige så sandsynligt, hvad er sandsynligheden for, at posen Therese får holder en jordnøddesmør og gel?sand ?ich og et æble?, |
|
|
Size of sample space:
(number of sandwich choices) • (number of chip choices) • (number of fruit choices) = 2 • 3 • 2 = 12
|
First, use the Fundamental Counting Principle to find the size of the sample space., |
|
|
Størrelsen af et areal til arrangementer:
(antallet af sandwich valg i event) • (antal chip valg i event) • (antal frugt valg i event) = |
For event-plads, de følger det samme princip. I dette tilfælde er der kun en sand .ich og et stykke frugt af interesse, men en af de tre typer chips er acceptabel., |
|
|
Svar |
|
Brug forhold til at finde sandsynligheden. |
Carrie vender fire mønter og tæller antallet af haler. Der er fire måder at få præcis en hale på: HHHT, HHTH, hthh og THHH. Hvad er sandsynligheden for, at Carrie får præcis en hale?,
A) ![]()
B) ![]()
C) ![]()
D) ![]()
Summary
Probability helps you understand random, unpredictable situations where multiple outcomes are possible., Det er et mål for sandsynligheden for en begivenhed, og det afhænger af forholdet mellem begivenhed og mulige resultater, hvis alle disse resultater er lige sandsynlige.