for at bruge referencevinkel-regnemaskinen skal du blot indtaste en hvilken som helst vinkel i vinkelboksen for at finde dens referencevinkel, som er den spidse vinkel, der svarer til den indtastede vinkel. Lommeregneren anvender automatisk de regler, vi gennemgår nedenfor.
Hvad er en referencevinkel, alligevel?
Forestil dig et koordinatplan. Lad os sige, at vi ønsker at tegne en vinkel, der er 144.på vores fly., Vi starter på højre side af axis-aksen, hvor klokken tre er på et ur. Vi roterer mod uret, som starter med at bevæge sig op. Vi fortsætter forbi 90 point-punktet (den øverste del af y-aksen), indtil vi kommer til 144.. Vi tegner en stråle fra oprindelsen, som er midten af flyet, til det punkt. Nu har vi en stråle, som vi kalder terminalsiden. Men vi er nødt til at tegne en mere stråle for at lave en vinkel. Vi har et valg på dette tidspunkt. Vores anden stråle skal være på axis-aksen. Hvis vi tegner det fra oprindelsen til højre side, har vi tegnet en vinkel, der måler 144.., Hvis vi tegner den til venstre, har vi tegnet en vinkel, der måler 36.. Denne anden vinkel er referencevinklen. Det er altid den mindste af de to vinkler, vil altid være mindre end eller lig med 90,, og det vil altid være positivt. Her er en animation, der viser en referencevinkel for fire forskellige vinkler, som hver er i en anden kvadrant. Bemærk, hvordan den anden stråle altid er på axis-aksen.
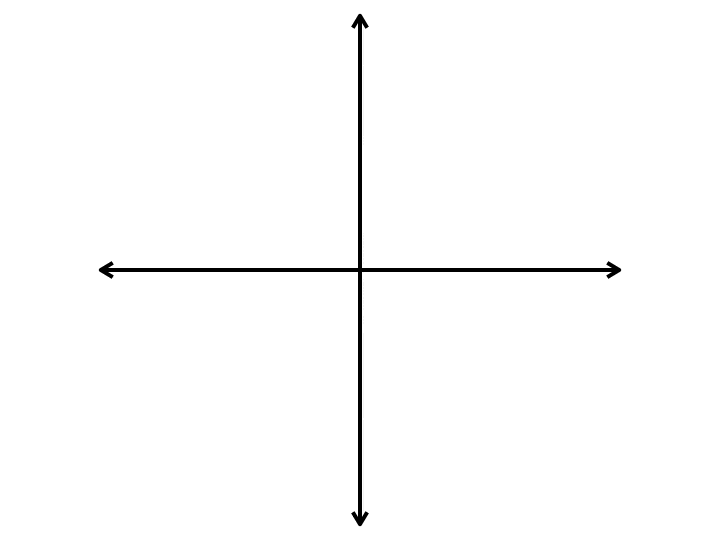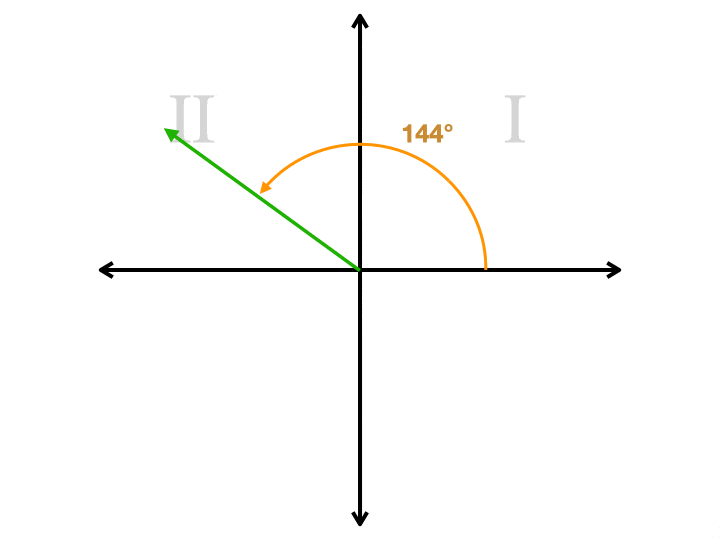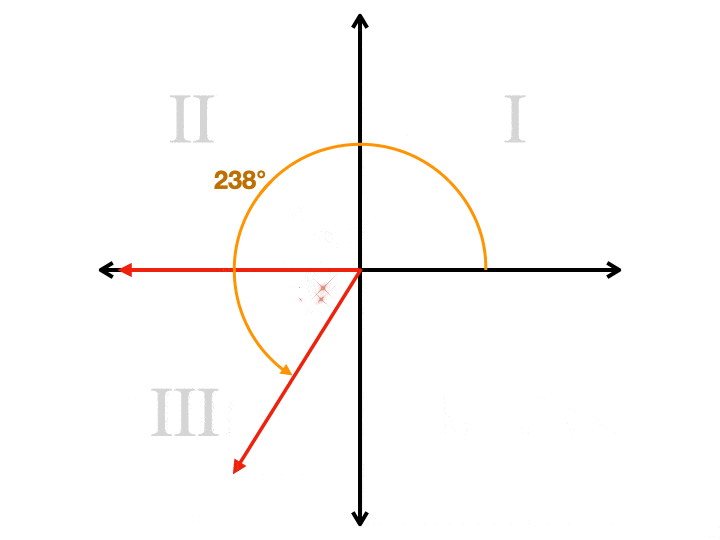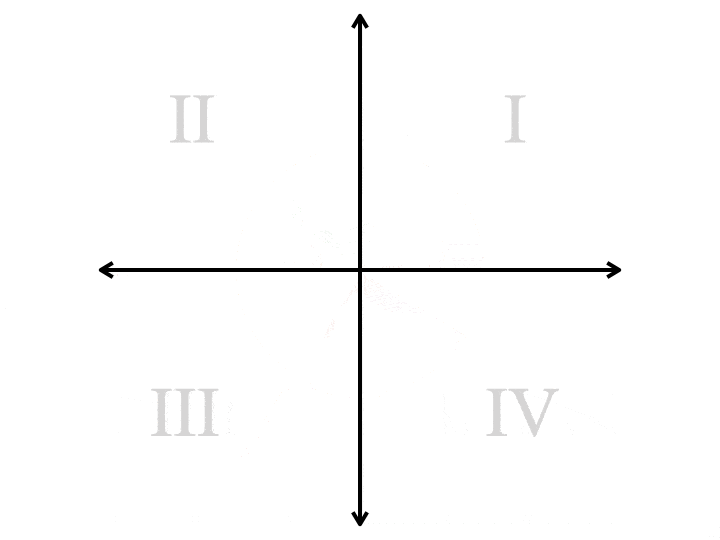
Hvordan er referencevinklen nyttig?
referencevinklen har altid de samme trig-funktionsværdier som den oprindelige vinkel. Bemærk ordværdierne der., Tegnet er muligvis ikke det samme, men værdien vil altid være. Dette er nyttigt til almindelige vinkler som 45 and og 60., som vi vil støde på igen og igen. Når vi kender deres sinus -, cosinus-og tangentværdier, kender vi også værdierne for enhver vinkel, hvis referencevinkel også er 45 or eller 60.. Hvad angår tegnet, skal du huske, at sinus er positiv i 1.og 2. kvadrant, og cosinus er positiv i 1. og 4. kvadrant.
Hvordan finder vi referencevinklen uden en lommeregner?
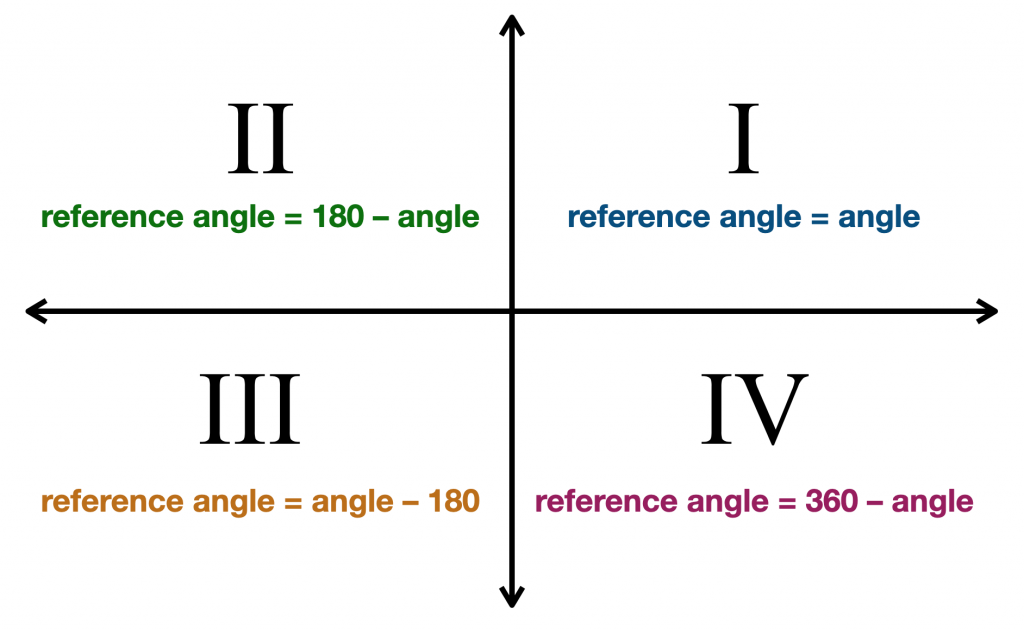
hvordan vi finder referencevinklen afhænger af kvadranten på terminalsiden.,
Når terminalsiden er i den første kvadrant (vinkler fra 0 to til 90.), er vores referencevinkel den samme som vores givne vinkel. Dette giver mening, da alle vinkler i den første kvadrant er mindre end 90.. Så hvis vores givne vinkel er 33., så er referencevinklen også 33..
Når terminalsiden er i den anden kvadrant (vinkler fra 90 to til 180.), er vores referencevinkel 180. minus vores givne vinkel. Så hvis vores givne vinkel er 110., er dens referencevinkel 180. – 110. = 70..,
Når terminalsiden er i den tredje kvadrant (vinkler fra 180.til 270.), er vores referencevinkel vores givne vinkel minus 180.. Så hvis vores givne vinkel er 214., er dens referencevinkel 214. – 180. = 34..
Når terminalsiden er i den fjerde kvadrant (vinkler fra 270.til 360.), er vores referencevinkel 360. minus vores givne vinkel. Så hvis vores givne vinkel er 332., er dens referencevinkel 360. – 332. = 28..
hvad hvis vores vinkel er større end 360??,
Når en vinkel er større end 360., betyder det, at den har drejet hele vejen rundt om koordinatplanet og fortsætter. For at finde dens referencevinkel skal vi først finde den tilsvarende vinkel mellem 0.og 360.. Dette er let at gøre. Vi fortsætter med at trække 360 fra det, indtil det er under 360. For eksempel, hvis vores vinkel er 544,, ville vi trække 360 from fra den for at få 184° (544° – 360° = 184°). Nu vil vi bemærke, at det er i den tredje kvadrant, så vi ville trække 180 from fra det for at finde ud af, at vores referencevinkel er 4..
hvad hvis vores vinkel er negativ?,
Når en vinkel er negativ, bevæger vi den anden retning for at finde vores terminalside. Dette betyder, at vi bevæger os med uret i stedet for mod uret, når vi tegner det. Eller vi kan beregne det ved blot at tilføje det til 360.. For eksempel, hvis vores givne vinkel er -110,, vil vi tilføje den til 360 to for at finde vores positive vinkel på 250° (-110° + 360° = 250°). Nu skulle vi se, at vi er i den tredje kvadrant og anvende denne regel for at finde vores referencevinkel (250° – 180° = 70°).