Public Key-Kryptering
i Modsætning til symmetrisk nøgle kryptografi, vi må ikke finde historiske bruge offentlig-nøgle kryptografi. Det er et relativt nyt koncept.
symmetrisk kryptografi var velegnet til organisationer som regeringer, militære og store finansielle selskaber var involveret i den klassificerede kommunikation.,
med spredningen af mere usikre computernetværk i de sidste par årtier følte man et reelt behov for at bruge kryptografi i større skala. Den symmetriske nøgle viste sig at være ikke-praktisk på grund af udfordringer, den stod overfor for nøglestyring. Dette gav anledning til de offentlige nøgle kryptosystemer.
processen med kryptering og dekryptering er vist i den følgende illustration −
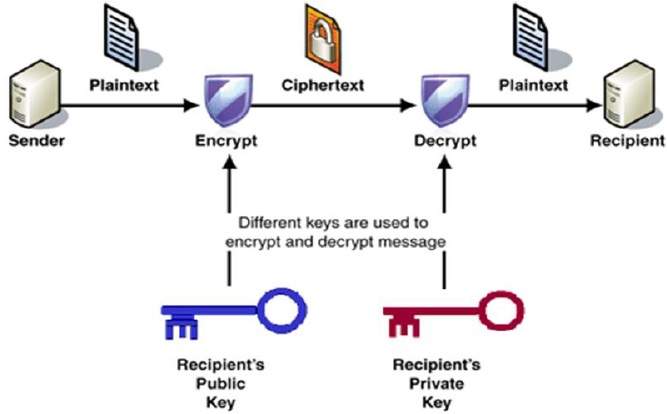
De vigtigste egenskaber ved public key-kryptering-ordningen er −
-
Forskellige taster bruges til kryptering og dekryptering., Dette er en egenskab, der sætter denne ordning anderledes end symmetrisk kryptering ordning.
-
hver modtager har en unik dekrypteringsnøgle, generelt benævnt hans private nøgle.
-
modtageren skal offentliggøre en krypteringsnøgle, kaldet hans offentlige nøgle.
-
en vis sikkerhed for ægtheden af en offentlig nøgle er nødvendig i denne ordning for at undgå forfalskning af modstander som modtager. Generelt involverer denne type kryptosystem betroet tredjepart, der attesterer, at en bestemt offentlig nøgle kun tilhører en bestemt person eller enhed.,
-
krypteringsalgoritmen er kompleks nok til at forbyde angriberen at udlede klarteksten fra cipherteksten og krypteringsnøglen (offentlig).
-
selvom private og offentlige nøgler er relateret matematisk, er det ikke muligt at beregne den private nøgle fra den offentlige nøgle. Faktisk er intelligent del af ethvert kryptosystem med offentlig nøgle i at designe et forhold mellem to nøgler.
Der er tre typer af offentlige nøgle kryptering ordninger., Vi diskuterer dem i følgende afsnit –
RSA-kryptosystem
dette kryptosystem er et af det oprindelige system. Det er stadig mest anvendte kryptosystem selv i dag. Systemet blev opfundet af tre lærde Ron Rivest, Adi Shamir, og Len Adleman og dermed, det betegnes som RSA kryptosystem.
Vi vil se to aspekter af RSA-kryptosystemet, for det første generation af nøglepar og for det andet krypteringsalgoritmer.,
generering af RSA-nøglepar
hver person eller en part, der ønsker at deltage i kommunikation ved hjælp af kryptering, skal generere et par nøgler, nemlig offentlig nøgle og privat nøgle. Den proces, der blev fulgt på i den generation af nøgler er beskrevet nedenfor −
-
Generere RSA-modul (n)
-
Vælg to store primtal, p og q.
-
Beregn n=p*q. For stærk ubrydelig kryptering, lad n være et stort antal, typisk minimum 512 bits.,
-
-
Find afledt tal (e)
-
nummer e skal være større end 1 og mindre end (p − 1)(1 − 1).
-
Der må ikke være nogen fælles faktor for e og (p − 1)(1 − 1) bortset fra 1. Med andre ord er to tal e og (p – 1)(1 – 1) coprime.
-
-
Dan den offentlige nøgle
-
parret af tal (n, e) danner den offentlige RSA-nøgle og offentliggøres.,
-
det er Interessant, om n er en del af den offentlige nøgle, vanskeligheder i factorizing et stort primtal sikrer, at angriberen ikke kan finde i begrænset tid de to primtal (p & q) anvendes til at opnå n. Dette er styrken af RSA.
-
-
Generere den private nøgle
-
Private Nøgle d, beregnes ud fra p, q og e. For givne n og e, der er unikt nummer, d.
-
Antal u er den inverse af e modulo (p – 1)(q – 1)., Dette betyder, at d er tallet mindre end (p-1) (1 – 1), således at når det multipliceres med e, er det lig med 1 modulo(p – 1) (. – 1).
-
Dette forhold skrives matematisk som følger −
-
ed = 1 mod (p − 1)(q − 1)
Den Udvidede Euklidisk Algoritme tager p, q og e som input og giver d som output.
eksempel
et eksempel på generering af RSA-nøglepar er angivet nedenfor. (For at lette forståelsen er primerne p & taken taget her små værdier. Praktisk set er disse værdier meget høje).,
-
Lad to primtal være p = 7 og 13 = 13. Således modul n = p. = 7 13 13 = 91.
-
Vælg e = 5, hvilket er et gyldigt valg, da der ikke er noget tal, der er fælles faktor på 5 og (p − 1)(5− 1) = 6 × 12 = 72, bortset fra 1.
-
parret af numre (n, e) = (91, 5) danner den offentlige nøgle og kan stilles til rådighed for alle, som vi ønsker at kunne sende os krypterede meddelelser.
-
Input p = 7, 13 = 13 og e = 5 til den udvidede euklidiske algoritme. Udgangen vil være d = 29.,
-
Kontroller, at den beregnede D er korrekt ved at beregne −
de = 29 × 5 = 145 = 1 mod 72
-
derfor er offentlig nøgle (91, 5) og private nøgler (91, 29).
kryptering og dekryptering
Når nøgleparet er genereret, er processen med kryptering og dekryptering relativt ligetil og beregningsmæssigt let.
interessant nok fungerer RSA ikke direkte på strenge af bits som i tilfælde af symmetrisk nøglekryptering. Det fungerer på numbers modulo n. derfor er det nødvendigt at repræsentere klarteksten som en række tal mindre end n.,
RSA-kryptering
-
Antag, at afsenderen ønsker at sende en SMS til en person, hvis offentlige nøgle er (n, e).
-
Den afsender, så repræsenterer den alm som en serie af tal mindre end n.
-
for At kryptere den første tekst-S, som er et tal modulo n. Krypteringen er simpel matematisk skridt, som −
C = Pe mod n
-
med andre ord, er det ciphertext C er lig med alm P ganget med sig selv e gange og derefter reduceret modulo n. Dette betyder, at C er også et tal mindre end n.,
-
Tilbage til vores Key Generation eksempel med almindelig tekst S = 10, får vi ciphertext C −
C = 105 mod 91
RSA Dekryptering
-
dekryptering for RSA er også meget ligetil. Antag, at modtageren af public-key par (n, e) har modtaget en cipherte Receivert C.
-
modtager hæver C til kraften i hans private nøgle d. resultatet modulo n vil være klartekst P.,
Plaintext = Cd mod n
-
at vende Tilbage igen til vores numerisk eksempel, den ciphertext C = 82 ville få dekrypteret til nummer 10 ved hjælp af den private nøgle 29 −
Plaintext = 8229 mod 91 = 10
RSA Analyse
sikkerheden af RSA afhænger af den stærke af de to separate funktioner. RSA-kryptosystemet er mest populært kryptosystem med offentlig nøgle, hvis styrke er baseret på den praktiske vanskelighed ved factoring af det meget store antal.,
-
Kryptering Funktion − Det betragtes som en en-vejs funktion til at konvertere tekst-til-maskine, og det kan kun vendes med den viden, private nøgle d.
-
Key Generation − Det er vanskeligt at bestemme en privat nøgle fra en offentlig RSA-nøgle svarer til factoring modulus n. En hacker kan således ikke anvende viden om en offentlig RSA-nøgle til at bestemme en RSA private key, medmindre han kan faktor n. Det er også en måde funktion, der går fra p & q-værdier til modulus n er let, men det omvendte er ikke muligt.,
Hvis en af disse to funktioner er bevist ikke envejs, vil RSA blive brudt. Faktisk, hvis der udvikles en teknik til factoring effektivt, vil RSA ikke længere være sikker.
styrken af RSA-kryptering går drastisk ned mod angreb, hvis tallet p og q ikke er store primtal og / eller valgt offentlig nøgle e er et lille antal.
ElGamal kryptosystem
sammen med RSA er der andre offentlige nøglekryptosystemer foreslået. Mange af dem er baseret på forskellige versioner af det diskrete Logaritmeproblem.,
ElGamal kryptosystem, kaldet elliptisk Kurvevariant, er baseret på det diskrete Logaritmeproblem. Det stammer styrken fra den antagelse, at den diskrete logaritmer ikke kan findes i praktisk tidsramme for et givet antal, mens den inverse operation af strømmen kan beregnes effektivt.
lad os gennemgå en simpel version af ElGamal, der fungerer med numbers modulo p. i tilfælde af elliptiske kurvevarianter er den baseret på helt forskellige talesystemer.,
Generation af ElGamal nøglepar
den Enkelte bruger af ElGamal kryptosystem genererer et nøglepar igennem som følger −
-
Valg af en stor prime s. Generelt et primtal 1024 til 2048 bits længde er valgt.
-
valg af generatorelement g.
-
dette tal skal være mellem 1 og p − 1, men kan ikke være noget tal.
-
Det er en generator af den multiplikative gruppe af de hele tal modulo p. Dette betyder, at for hvert heltal m co-primtal p, der er et heltal k, sådan at gk=a mod n.,
for eksempel er 3 generator af gruppe 5 (55= {1, 2, 3, 4}).
-
| N | 3n | 3n mod 5 |
|---|---|---|
| 1 | 3 | 3 |
| 2 | 9 | 4 |
| 3 | 27 | 2 |
| 4 | 81 | 1 |
-
Valg af den private nøgle. Den private nøgle is er et tal større end 1 og mindre end p-1.
-
Computing del af den offentlige nøgle., Værdien y beregnes ud fra parametrene p, g og den private nøgle.som følger −
y = gx mod p
-
opnåelse af offentlig nøgle. ElGamal public key består af de tre parametre (p, g, y).Antag for eksempel at p = 17 og at g = 6 (det kan bekræftes, at 6 er en generator af gruppe1717). Den private nøgle x kan være et hvilket som helst tal større end 1 og mindre end 71, så vi vælger = = 5. Værdien y beregnes derefter som følger –
y = 65 mod 17 = 7
-
således er den private nøgle 62 og den offentlige nøgle (17, 6, 7).,
kryptering og dekryptering
genereringen af et Elgamal nøglepar er forholdsvis enklere end den tilsvarende proces for RSA. Men kryptering og dekryptering er lidt mere kompleks end RSA.
ElGamal Kryptering
Antag, at afsenderen ønsker at sende en tekst til en person, hvis ElGamal offentlige nøgle er (p, g, y), så −
-
Afsender repræsenterer den alm som en serie af tal modulo p.
-
for At kryptere den første tekst-S, som er repræsenteret som et tal modulo p., Kryptering proces at opnå den ciphertext C er som følger −
- Tilfældigt at generere et tal k;
- Beregne to værdier, C1 og C2, hvor −
C1 = gk mod pC2 = (P*yk) mod p
-
Send ciphertext C, der består af to separate værdier (C1, C2), sendt sammen.,
-
Henvise til vores ElGamal-tasten generation eksemplet ovenfor, alm P = 13 er krypteret som følger −
- Tilfældigt at generere et tal, siger k = 10
- Beregne de to værdier, C1 og C2, hvor −
C1 = 610 mod 17C2 = (13*710) mod 17 = 9
-
Send ciphertext C = (C1, C2) = (15, 9).,
ElGamal Dekryptering
-
for At dekryptere ciphertext (C1, C2) bruger den private nøgle x, følgende to skridt er taget −
-
Beregne den modulære inverse af (C1)x modulo p, som er (C1)-x , normalt omtalt som dekryptering faktor.,
-
hent almindelig tekst ved hjælp af følgende formel
-
C2 × (C1)-x mod p = Plaintext
-
I vores eksempel, til at dekryptere ciphertext C = (C1, C2) = (15, 9) ved hjælp af den private nøgle x = 5, dekryptering faktor er,
15-5 mod 17 = 9
-
Ekstrakt af almindelig tekst, P = (9 × 9) mod 17 = 13.
ElGamal − analyse
i ElGamal-systemet har hver bruger en privat nøgle.. og har tre komponenter af offentlig nøgle-prime modul p, generator g og offentlig Y = g. mod p., Styrken af ElGamal er baseret på vanskeligheden ved diskret logaritme problem.
den sikre nøglestørrelse er generelt > 1024 bits. I dag bruges endda 2048 bits lang nøgle. På behandlingshastighedsfronten er Elgamal ret langsom, den bruges hovedsageligt til nøgleautentificeringsprotokoller. På grund af højere behandlingseffektivitet bliver elliptiske Kurvevarianter af ElGamal stadig mere populære.,
elliptisk Kurvekryptografi (ECC)
elliptisk Kurvekryptografi (ecc) er et udtryk, der bruges til at beskrive en pakke kryptografiske værktøjer og protokoller, hvis sikkerhed er baseret på specielle versioner af det diskrete logaritmeproblem. Det bruger ikke tal modulo p.
ECC er baseret på sæt tal, der er forbundet med matematiske objekter kaldet elliptiske kurver. Der er regler for at tilføje og beregne multipla af disse tal, ligesom der er for tal modulo p.,
ECC indeholder en varianter af mange kryptografiske ordninger, der oprindeligt var designet til modulære numre såsom ElGamal kryptering og Digital signatur algoritme.
det antages, at det diskrete logaritmeproblem er meget sværere, når det anvendes på punkter på en elliptisk kurve. Dette beder om at skifte fra tal modulo p til punkter på en elliptisk kurve. Også et tilsvarende sikkerhedsniveau kan opnås med kortere nøgler, hvis vi bruger elliptiske kurvebaserede varianter.,
Den kortere nøgler resultere i to fordele −
- Lethed centrale forvaltning
- Effektiv beregning
Disse fordele gør elliptisk-kurve-baserede varianter af kryptering ordningen særdeles attraktiv for anvendelse, hvor it-ressourcer er begrænset.
RSA og ElGamal Ordninger – En Sammenligning
Lad os kort sammenligne RSA og ElGamal ordninger på de forskellige aspekter.
| RSA | ElGamal |
|---|---|
| Det er mere effektivt for kryptering. | det er mere effektivt til dekryptering., |
| det er mindre effektivt til dekryptering. | det er mere effektivt til dekryptering. |
| for et bestemt sikkerhedsniveau kræves lange nøgler i RSA. | for det samme sikkerhedsniveau kræves meget korte nøgler. |
| det er almindeligt accepteret og brugt. | det er nyt og ikke meget populært på markedet. |