Correlational Forskning: Søger Relationer Mellem Variabler
I modsætning til beskrivende forskning, der primært er udformet til at give statiske billeder, correlational forskning indebærer måling af to eller flere relevante variable, og en vurdering af forholdet mellem disse variabler., For eksempel, variablerne i højde og vægt er systematisk relateret (korreleret) fordi højere mennesker generelt vejer mere end kortere mennesker. På samme måde er studietid og hukommelsesfejl også relateret, fordi jo mere tid en person får til at studere en liste over ord, jo færre fejl vil han eller hun lave. Når der er to variabler i forskningsdesignet, kaldes en af dem forudsigelsesvariablen og den anden resultatvariablen., Forskning design kan visualiseres som denne, hvor den buede pil repræsenterer den forventede korrelation mellem de to variabler:
Figur 2.2.2

En måde at organisere data fra en correlational undersøgelse med to variabler er, at plotte værdierne for hver af de målte variable ved hjælp af en scatter plot. Som du kan se i figur 2.10 “eksempler på Scatter Plots”, er et scatter plot et visuelt billede af forholdet mellem to variabler., Et punkt er afbildet for hver enkelt i skæringspunktet mellem hans eller hendes scoringer for de to variabler. Når sammenhængen mellem variablerne på scatter plot let kan tilnærmes med en lige linje, som i dele (A) og (B) i figur 2.10 “eksempler på Scatter Plots”, siges variablerne at have et lineært forhold.
når den lige linje angiver, at personer, der har værdier over gennemsnittet for en variabel, også har en tendens til at have værdier over gennemsnittet for den anden variabel, som i del (A), siges forholdet at være positivt lineært., Eksempler på positive lineære forhold inkluderer dem mellem højde og vægt, mellem uddannelse og indkomst og mellem alder og matematiske evner hos børn. I hvert tilfælde har folk, der scorer højere på en af variablerne, også en tendens til at score højere på den anden variabel. Negative lineære relationer, derimod, som vist i del (B), opstår, når over gennemsnittet værdier for en variabel tendens til at være forbundet med Under gennemsnittet værdier for den anden variabel., Eksempler på negative lineære forhold inkluderer dem mellem et barns alder og antallet af bleer, barnet bruger, og mellem praksis og fejl, der er foretaget på en læringsopgave. I disse tilfælde har folk, der scorer højere på en af variablerne, en tendens til at score lavere på den anden variabel.
forhold mellem variabler, der ikke kan beskrives med en lige linje, kaldes ikke-lineære forhold. Del (C) i figur 2.10 “eksempler på Scatter Plots” viser et fælles mønster, hvor fordelingen af punkterne er hovedsagelig tilfældig., I dette tilfælde er der overhovedet ikke noget forhold mellem de to variabler, og de siges at være uafhængige. Dele (d) og (e) i figur 2.10 “eksempler på Scatter Plots” viser foreningsmønstre, hvor selv om der er en forening, er punkterne ikke godt beskrevet af en enkelt lige linje. For eksempel viser del (d) den type forhold, der ofte opstår mellem angst og ydeevne., Stigninger i angst, fra lave til moderate niveauer er forbundet med ydelsen stiger, mens stigninger i angst fra moderate til høje niveauer er forbundet med fald i ydeevne. Forhold, der ændrer sig i retning og således ikke beskrives af en enkelt lige linje, kaldes krumme forhold.
Figur 2.10 Eksempler på Scatter Plots
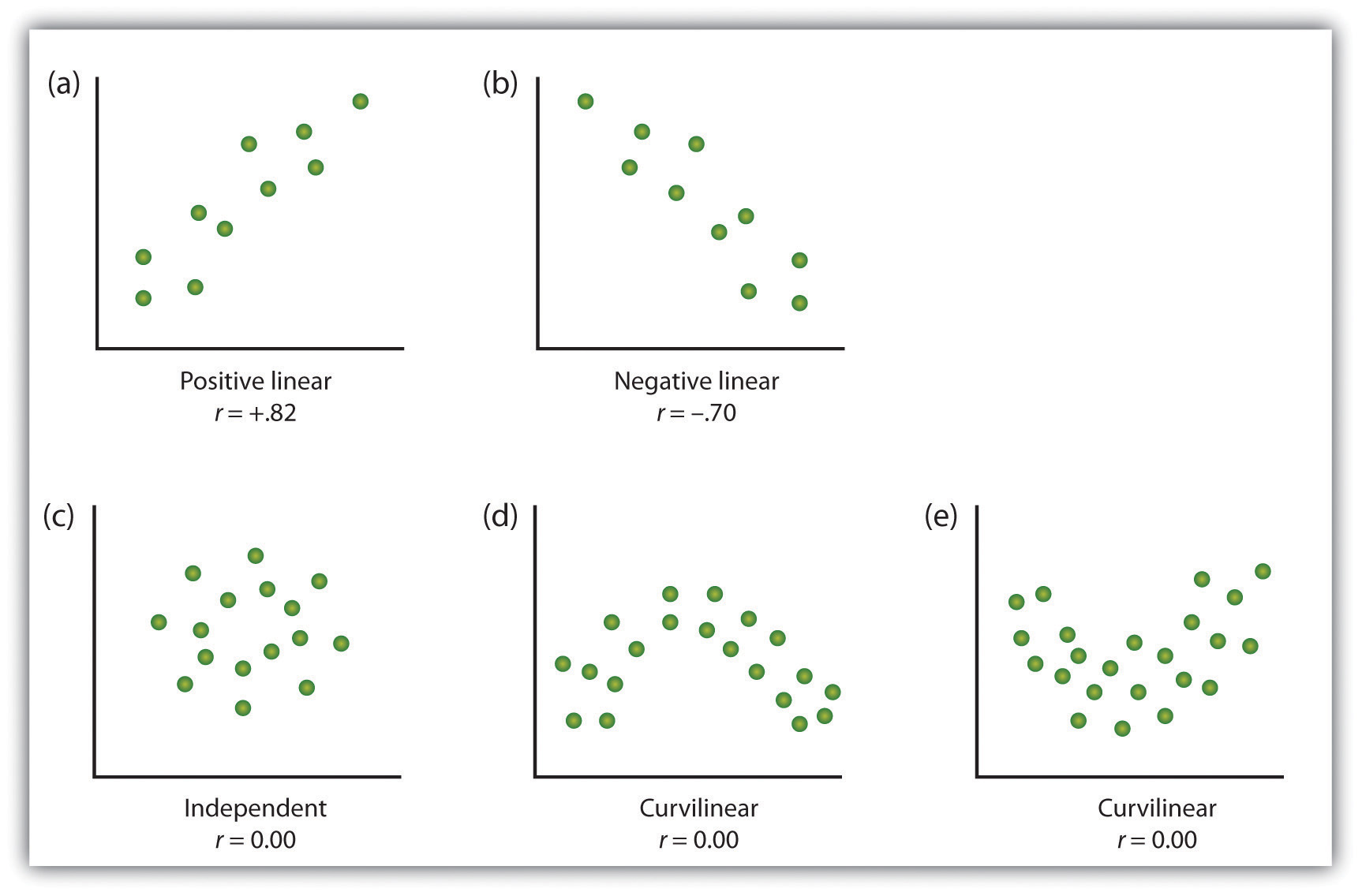
Nogle eksempler på relationer mellem to variable, som vist i scatter plots., Bemærk, at Pearson-korrelationskoefficienten (r) mellem variabler, der har krumme forhold, sandsynligvis vil være tæt på nul.
tilpasset fra Stangor, C. (2011). Forskningsmetoder for adfærdsvidenskab (4.udgave.). Mountain Vie., CA: Cengage.
den mest almindelige statistiske måling af styrken af lineære forhold mellem variabler er Pearson-korrelationskoefficienten, som symboliseres med bogstavet r. værdien af korrelationskoefficienten varierer fra r = -1,00 til r = +1,00., Retningen af det lineære forhold er angivet ved tegn på korrelationskoefficienten. Positive værdier af r (såsom r = .54 eller r = .67) angiver, at forholdet er positivt lineært (dvs. mønsteret af prikkerne på scatterplottet løber fra nederste venstre til øverste højre), mens negative værdier af r (såsom r = –.30 eller r = -.72) angiver negative lineære forhold (dvs.prikkerne løber fra øverste venstre til nederste højre). Styrken af det lineære forhold indekseres af afstanden af korrelationskoefficienten fra nul (dens absolutte værdi)., For eksempel r = –.54 er et stærkere forhold end r =.30, og r = .72 er et stærkere forhold end r = –.57. Fordi Pearson-korrelationskoefficienten kun måler lineære forhold, variabler, der har krumme forhold, beskrives ikke godt af r, og den observerede korrelation vil være tæt på nul.
det er også muligt at studere forhold mellem mere end to mål på samme tid., Et forskningsdesign, hvor mere end en forudsigelsesvariabel bruges til at forudsige en enkelt resultatvariabel, analyseres gennem multipel regression (Aiken & Vest, 1991). Multipel regression er en statistisk teknik, baseret på korrelationskoefficienter blandt variabler, der gør det muligt at forudsige en enkelt resultatvariabel fra mere end en forudsigelsesvariabel. For eksempel viser figur 2.11 “forudsigelse af jobpræstation fra tre forudsigelsesvariabler” en multipel regressionsanalyse, hvor tre forudsigelsesvariabler bruges til at forudsige et enkelt resultat., Brugen af multipel regressionsanalyse viser en vigtig fordel ved korrelationsforskningsdesign—de kan bruges til at forudsige en persons sandsynlige score på en resultatvariabel (f.jobpræstation) baseret på viden om andre variabler.
Figur 2.11 Forudsigelse af arbejdsindsats Fra Tre Prædiktor-Variable
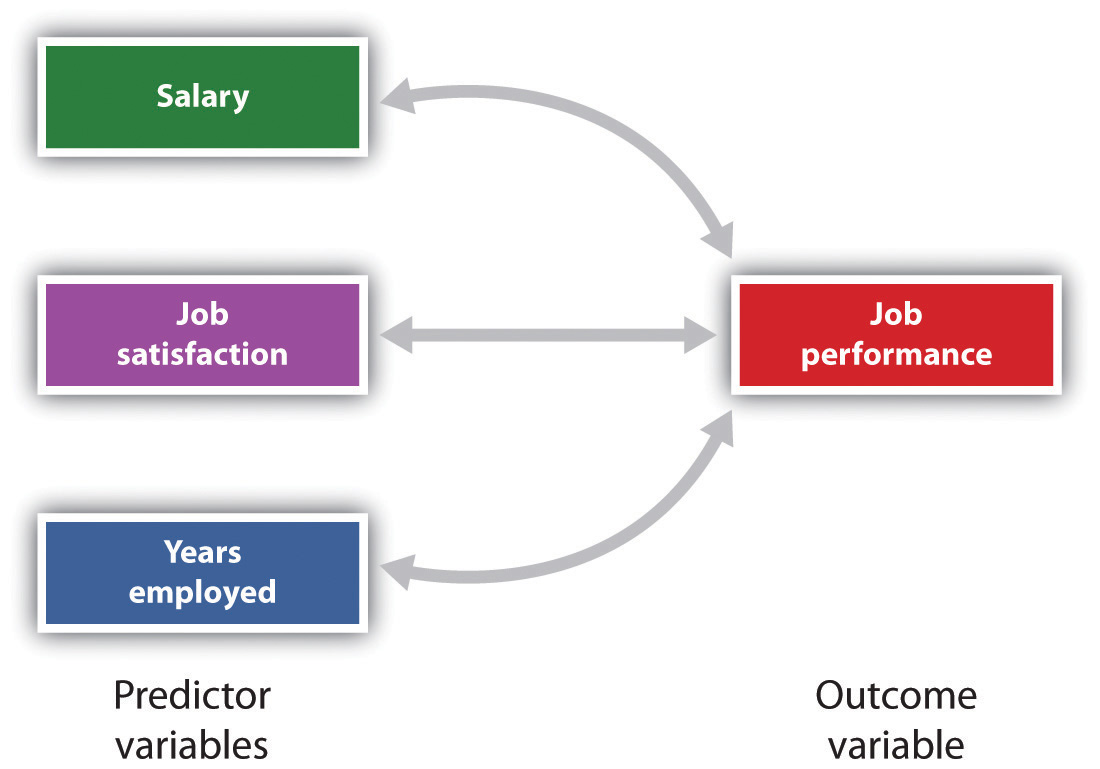
Multiple regression giver forskerne mulighed for at forudsige de scorer på et enkelt resultat-variabel ved hjælp af mere end en prædiktor variabel.,
en vigtig begrænsning af korrelationsforskningsdesign er, at de ikke kan bruges til at drage konklusioner om årsagssammenhænge mellem de målte variabler. Overvej for eksempel en forsker, der har antaget, at det at se voldelig opførsel vil medføre øget aggressiv leg hos børn. Han har indsamlet, fra en stikprøve på fjerde klassetrin børn, et mål for, hvor mange voldelige tv-shows hvert barn visninger i løbet af ugen, samt et mål for, hvor aggressivt hvert barn spiller på skolens legeplads., Fra sine indsamlede data opdager forskeren en positiv sammenhæng mellem de to målte variabler.
selvom denne positive korrelation ser ud til at understøtte forskerens hypotese, kan det ikke tages for at indikere, at visning af voldeligt tv forårsager aggressiv adfærd. Selv om forskeren er fristet til at antage, at ser voldelige tv-årsager aggressive spil,
Figur 2.2.2

der er andre muligheder., En alternativ mulighed er, at årsagsretningen er nøjagtigt modsat det, der er blevet antaget. Måske børn, der har opført sig aggressivt på skolen udvikle resterende spænding, der fører dem til at have lyst til at se voldelige tv-shows på hjemme:
Figur 2.2.2

Selv om denne mulighed kan synes mindre sandsynligt, der er ingen måde at udelukke muligheden for, at en sådan omvendt årsagssammenhæng på baggrund af det observerede korrelation., Det er også muligt, at både kausal retninger opererer, og at de to variabler årsag hinanden:
Figur 2.2.2

Stadig en anden mulig forklaring på den observerede korrelation er, at det er blevet produceret af tilstedeværelsen af en fælles-kausale variabel (også kendt som en tredje variabel)., En fælles-kausal variabel er en variabel, der ikke er en del af forskningshypotesen, men som forårsager både forudsigeren og resultatvariablen og dermed frembringer den observerede sammenhæng mellem dem. I vores eksempel en potentiel fælles-kausal variabel er disciplin stil af børnenes forældre. Forældre, der bruger en hård og straffende disciplin stil kan producere børn, der begge kan lide at se voldelige tv, og som opfører sig aggressivt i forhold til børn, hvis forældre bruger mindre hård disciplin:
Figur 2.2.,2
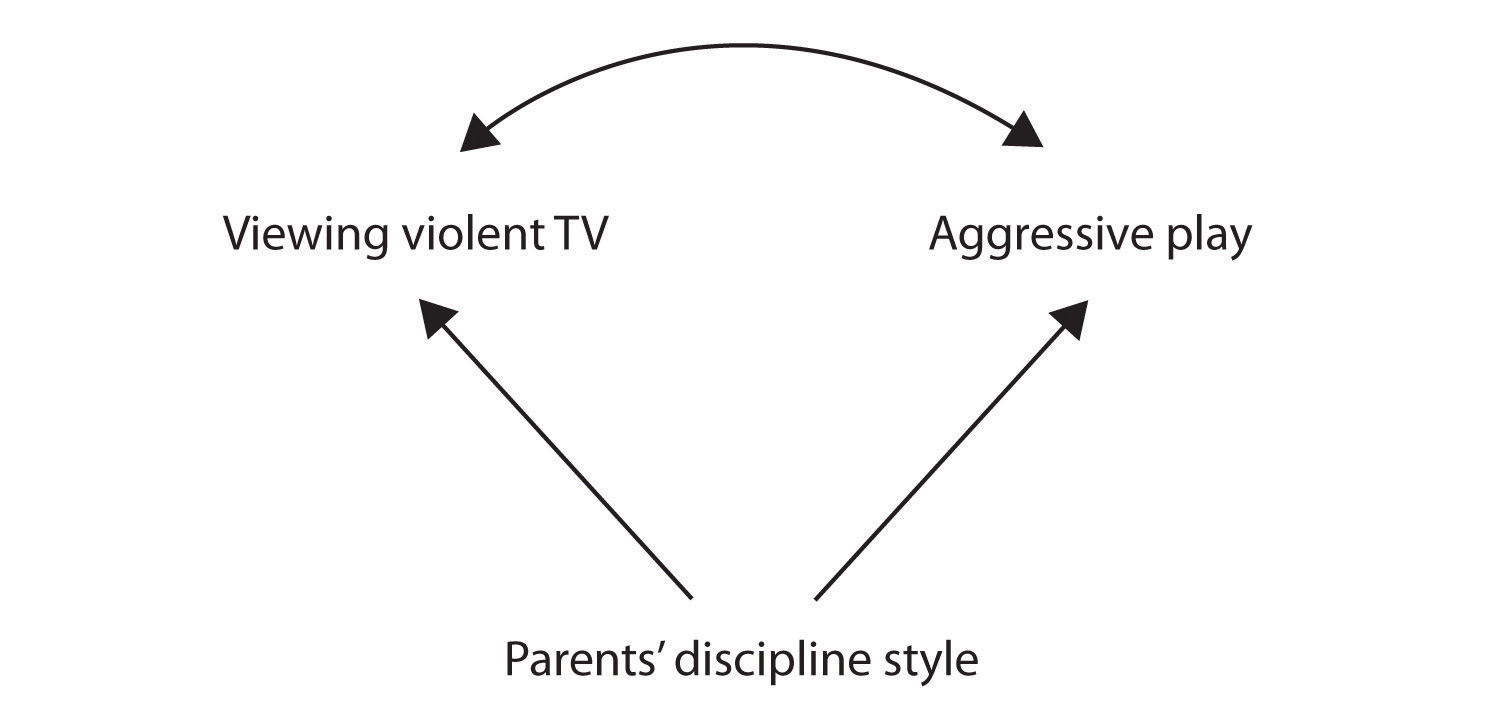
I dette tilfælde, tv-visning og aggressiv spiller vil være positivt korreleret (som angivet af den buede pil mellem dem), selv om hverken det ene skyldes det andet, men de var begge forårsaget af disciplin stil af forældrene (lige pile). Når forudsigelses-og resultatvariablerne begge er forårsaget af en fælles-kausal variabel, det observerede forhold mellem dem siges at være falsk., Et falsk forhold er et forhold mellem to variabler, hvor en fælles-kausal variabel producerer og “forklarer væk” forholdet. Hvis virkningerne af den fælles-kausale variabel blev taget væk eller kontrolleret for, ville forholdet mellem forudsigeren og resultatvariablerne forsvinde. I eksemplet kan forholdet mellem aggression og tv-visning være falsk, fordi forholdet mellem tv-visning og aggressiv adfærd kan forsvinde ved at kontrollere virkningen af forældrenes disciplinerende stil.,
fælles-kausale variabler i korrelationsforskningsdesign kan betragtes som “mysterium” – variabler, fordi deres tilstedeværelse og identitet normalt ikke er ukendt for forskeren, da de ikke er målt. Da det ikke er muligt at måle hver variabel, der kan forårsage både forudsigelses-og resultatvariablerne, er eksistensen af en ukendt fælles-kausal variabel altid en mulighed. Af denne grund står vi tilbage med den grundlæggende begrænsning af korrelationsforskning: korrelation demonstrerer ikke årsagssammenhæng., Det er vigtigt, at når du læser om korrelationsforskningsprojekter, husker du muligheden for falske forhold, og sørg for at fortolke resultaterne korrekt. Selvom korrelationsforskning undertiden rapporteres som demonstrerende kausalitet uden at nævne muligheden for omvendt årsagssammenhæng eller almindelige årsagsvariabler, er informerede forbrugere af forskning som dig opmærksomme på disse fortolkningsproblemer.
samlet set har korrelationsforskningsdesign både styrker og begrænsninger., En styrke er, at de kan bruges, når eksperimentel forskning ikke er mulig, fordi forudsigelsesvariablerne ikke kan manipuleres. Korrelationsdesign har også fordelen ved at give forskeren mulighed for at studere adfærd, som den forekommer i hverdagen. Og vi kan også bruge korrelationsdesign til at lave forudsigelser—for eksempel at forudsige fra scoringerne på deres batteri af test succes for jobpraktienter under en træningssession. Men vi kan ikke bruge sådanne korrelationsinformation til at afgøre, om træningen forårsagede bedre jobpræstation. Til det er forskere afhængige af eksperimenter.,